Rational Exponents & Radical Form
Polynomials
Mixture
Volume
More Volume
100
Without using any numbers, write down the formulas for both Rational Exponent Form = Radical Root Form
x^(frac(a)(b)) = (root(b)(x))^a
100
(5x-x^2+8) + (8 - x^4 + 3x^2)
-x^4 + 2x^2 + 5x + 16
100
Simplify: (x+4)^2
x^2 + 8x + 16
100
Find the Volume:
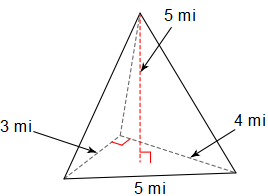
V = 10 mi^3
100
Find the volume of the composite figure. Round to the nearest tenth.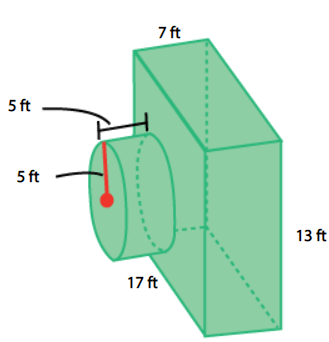
1939.7 ft3
200
What was wrong with this list of steps?
8^(frac(4)(3)) = (3root()(8))^4 = (8.485)^4 = 5184
They did not use the correct root!
200
(-6x^3 + 5x^2 -3)-(2x^3 -4x^2 -3x +1)
-8x^3+9x^2+3x -4
200
A Cylinder has a radius of 5 yds and a height of 6 yds, What is the Volume of the Cylinder?
V≈471.24 yd^3
200
A Cylinder has a diameter of 169 and a height of 8,What is the Volume of the Cylinder?
V≈179454
200
Find the volume of the composite figure. Round to the nearest tenth.
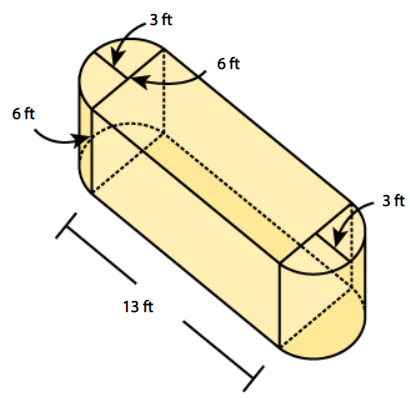
637.7 ft3
300
root(6)(15625)= ?
5
300
(x^2 - 4)-(2x^2 + 4x -6)
-x^2 -4x +2
300
Determine the area & perimeter of a rectangle whose length is 3x+1 and width is 2x
P = 10x + 2 units
A = 6x2 + 2x units2
300
A Cone has a Diameter of 10 and a height of 5, What is the volume of the Cone?
V≈130.9
300
Find the volume of the composite figure. Round the answer to the nearest tenth.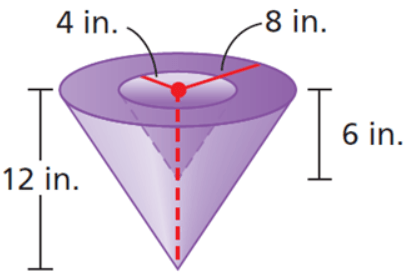
703.7 in3
400
Rewrite and simplify the following term:
(∜81)^5
(∜81)^5 = 81^[\frac(5)(4)] = 243
400
Find the area and perimeter of the square with a side measurement of
5x^4y^2
Perimeter:
20x^4y^2
Area:
25x^8y^4
400
Given a Cube with a side length of (2x-1) in, What is the Volume of the Cube?
V=
(8x^3 + 4x^2 -2x -1)
in^3
400
Given a Sphere with the diameter of 20cm, What is the Volume of this Sphere?
V≈4188.79
400
Find the volume of the composite figure. If necessary, round to the nearest tenth.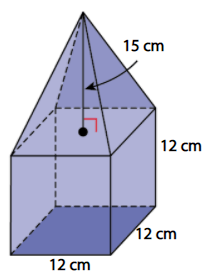
2448 cm3
500
List out all of the possible steps in rewriting and simplifying the following term:
16^[\frac(3)(4)]
16^[\frac(3)(4)] = (∜16)^3 = (2)^3 = 8
500
Find the area and perimeter of the following rectangular fence with two measurements of (x -1) and (4x-1) miles.
Perimeter: 10x -4
Area:
(4x^2 -5x +1 )mi^2
500
Find the Volume of the following figure (using feet as your units):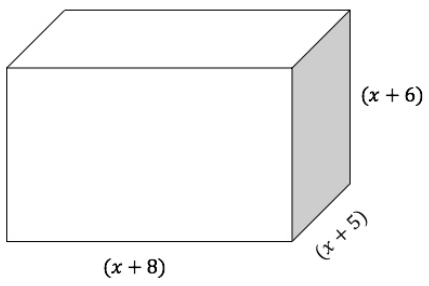
V = (x^3+19x^2 + 118x + 240)ft^3
500
Find the volume.
294m^3
500
Find the volume of the composite figure. The figure shown is a cone with a hole in the shape of half a sphere. Round the answer to the nearest tenth.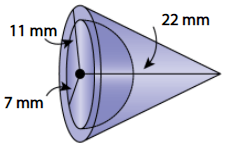
2069.3 mm3