Calculus Vocab
Derivatives
Miscellaneous
Integrals
Calculus History
100
The branch of mathematics that deals with the finding and properties of derivatives and integrals of functions, by methods originally based on the summation of infinitesimal differences.
calculus.
100
Derivative of: 7
What is: 0
100
When you integrate, you find this under the graph of a function bounded by a closed interval.
area.
100
∫sin(x)dx
What is: -cos(x) + C
100
Calculus is the mathematical study of this.
rates of change.
200
This is the value that a function approaches as the input approaches a value.
limit.
200
Derivative of: x3 + 5x2 + x + 1
What is: 3x2 + 10x + 1
200
\frac{d}{dx} (\sin^2x +cos^2x)
0
200
∫(x)dx
What is: 1/2x^2 + C
200
The word "calculus" comes from this language and means a small stone used for counting.
Latin.
300
What rule is this: h(x) = f(g(x)) then h'(x) = f'(g(x))(g'(x))
Chain Rule
300
Derivative of: ln x
What is: 1/x
300
The process of reversing differentation
antidifferentiation
300
∫sin(x)dx
-cos (x) + C
300
This notation is named after a famous mathematician. Example: d/dx(x^2) = 2x
Leibniz notation.
400
Given the x(t) is the position of the particle, what is the first then second derivative with respect to time?
Velocity and acceleration
400
Derivative of: -cos (x)
sin(x)
400
What is this rule
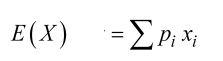
mean or expected value for random variable X
.
400
∫(1/x)dx
What is: ln(x) + C
400
Gottfried Leibniz and this British scientist are credited with the invention of calculus.
Isaac Newton.
500
This rule/method is used to find the derivative of indeterminate forms.
What is L'Hospital's Rule?
500
Derivative of: sin x + ln (x2)
cos (x) + 2/x ?
500
To find the derivative of the inverse function
(f^{-1})'f(x) =
What is
\frac{1}{f'(x)}
?
500
∫(x^2)dx
What is: 1/3x^3 + C
500
Many mathematical ideas, including calculus, are said to have been started by this philosopher around 580-500 B.C.
Pythagoras.