Straight Line Graphs
Circles
Differentiation
Maths
Miss Reid
100
The line L passes through the points:
(2, 1) and (4, -5)
Find an equation for line L
3x + y - 7 = 0
OR
y = -3x + 7
100
The circle C has centre (2, 5) and passes through the point (4, 9).
Find an equation for C
(x - 2)2 + (y - 5)2 = 20
100
y = 2x3 + 5x2 - 7x + 10
Find the gradient of the curve when x = 2
37
100
How many teachers are in the maths department?
9
100
How old is Miss Reid?
28
200
A line has the equation
6x + 7y - 23 = 0
It crosses the x-axis at point A, the y-axis at point B and O is the origin.
Find the area of triangle AOB
529/84
200
The circle C has the equation:
x2 + y2 - 2x + 6y = 26
Find the centre and radius
Centre (1, -3)
Radius = 6
200
y=3x+1/x
Find the x coordinates of the points where the gradient is zero
x=+-\sqrt(1/3)
200
Who is the newest member of the maths department?
Mr Pickup
200
Which country is Miss Reid going on holiday to for Christmas?
Canada
300
The point A has coordinates (-2, 3) and point B has coordinates (4, -7)
The perpendicular bisector of AB intersects the line
y = 2x + 1 at the point P.
Find the coordinates of P
(-3/7 , 1/7 )
300
The circle C has centre (2, 5) and radius 7
The line y = 3x - 1 intersects C at the points A and B. Find the exact coordinates of A and B
((20+7\sqrt 10)/10 , (50+21\sqrt 10)/10)
and
((20-7\sqrt 10)/10, (50-21\sqrt 10)/10)
300
A curve has equation y=x^3+px^2+qx-5
The curve passes through the point A(2, 1)
The gradient of the curve at A is 5
Find the value of p and q
p = -3
q = 5
300
Who is the youngest member of the maths department?
Mr Tyrrell
300
How many siblings does Miss Reid have?
3
400
The points A and B have coordinates (-1, k+2) and (2k-3, 8)
Given that the gradient is 1/3
Find the equation of the perpendicular bisector of AB. Give your answer in the form ax+by+c=0
3x + y - 13 = 0
400
The circle C has centre (5, k), where k is a constant
The line y = 2x + 1 is a tangent to the circle C, touching C at the point A(3, 7).
Find an equation for C
(x - 5)2 + (y - 6)2 = 5
400
a curve has equation f(x)=(x+3)(x-2)^2
Find the coordinates of the curve's local minimum
(2, 0)
400
Who is the longest serving member of the department?
Ms Malkin
400
What car does Miss Reid drive?
(Make, model and colour)
A blue Seat Ibiza
500
Point C has coordinates (2, c) and point D has coordinates (d, 8)
The perpendicular bisector of CD has equation
3y + x = 10
Find c and d
c = -4
d = 6
500
The line y = mx - 2 is a tangent to the circle
x2 + 6x + y2 - 8y + 5 = 0
Find two possible values of m, giving your answer in exact form
m = (18+10\sqrt 5)/11
OR
m = (18-10\sqrt 5)/11
500
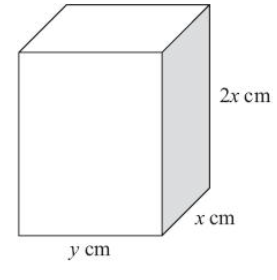
A solid brick in the shape of a cuboid has measurements 2x cm by x cm by y cm.
The total surface area of the brick is 600cm2
Given that x can vary, find the maximum value the Volume can take.
943cm3
500
What sport does Mr Tomlin play?
Softball
500
In which UK city was Miss Reid born?
Southampton