Linear Relationships
Angle Relationships and Properties of Geometrical Figures
Ratios and Rates
100
What are the coordinates of D?
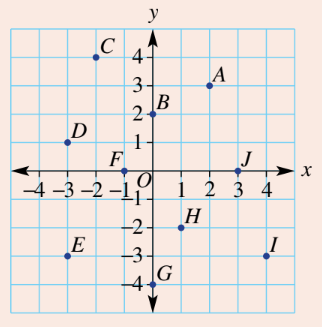
-3, 1
100
Classify this triangle by side (scalene, isosceles, equilateral) and angle (acute, right, obtuse) and find the value of a.
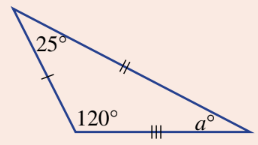
Scalene, Obtuse Triangle
a = 35 degrees
100
Simplify the ratio 36 : 24.
3 : 2
200
Write the gradient and y-intercept for the graph of the rule y = -3x + 7.
Gradient = -3
y-intercept = 7
200
Find the value of a. Give a reason for your answer.
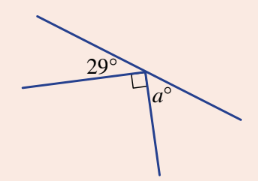
a = 61 degrees (angles on a straight line)
200
Express $650 for 13 hours in simplest form.
$50/hr
300
For the rule y = 2x + 2, create a table of values from -3 to 3 and plot to draw a straight line graph.
300
Find the interior angle sum of a nonagon.
1260 degrees
300
For a scale of 1 : 1000, find the real length (in metres) if the scale length is 2.7 cm.
27 m
400
Write the rule for this table of values.
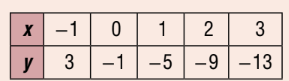
y = -4x - 1
400
Find the value of a and b in this quadrilateral.
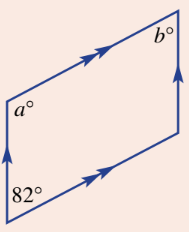
a = 98 degrees
b = 82 degrees
400
Divide $1445 in the ratio 4 : 7 : 6.
$340 : $595 : $510
500
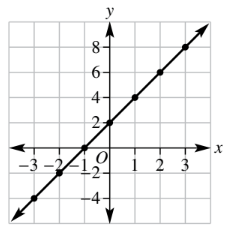
Find the gradient of this line.
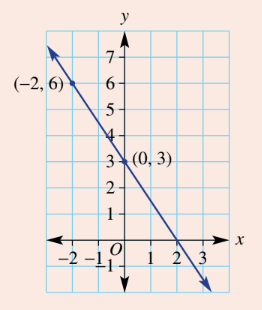
m = -3/2
500
Find the value of a.
a = 67 degrees
500
How far does Siri ride her bike if she rides at 4.5km/h for 90 minutes?
6.75 km
600
Find the x- and y- intercept for the graphs of the rule y = 2x - 12.
(6, 0) and (0, -12)
600
Find the value of a.
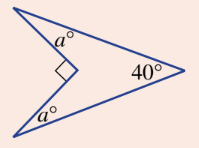
a = 25 degrees
600
Convert 6 m/s into km/h.
21.6 km/h
700
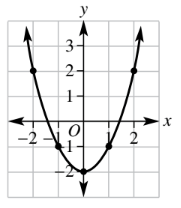
Using a table of values with x-values between -2 and 2, draw a curve for the rule y = x2 - 2.
700
Find the value of x in this diagram.
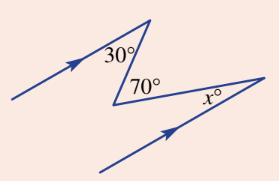
x = 40 degrees
700
Tap 1 fills the pool in 12 hours, while tap 2 fills the same pool in 15 hours. How long does it take to fill this pool if both taps are used?
6 2/3 hours