Congruency & Similarity
Area
Composite
Volume and Capacity
Pythagoras
100
Name the 5 Congruency Tests:
AAS
SAS
RHS
SSS
AAA
100
What is the area and circumference formula for a Circle?
A = ∏r2
C = 2∏r
100
Describe what a composite shape is.
a new shape created with 2 or more basic shapes.
100
How many cm3 in a mL?
1cm3 = 1mL
100
What does the C represent in the Pythagoras Theorem?
C = Hypotenuse
200
What symbol do you use to show that 2 shapes are congruent?
200
Find the circumference of the circle below:
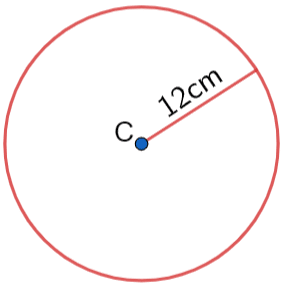
C = 2∏r
C = 2 x ∏ x 12cm
C = 75.40cm
200
What 2 shapes create the following composite shape?
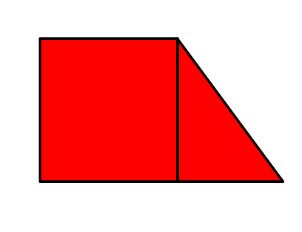
Square & Right-Angled Triangle
(Accept Square and Triangle)
200
Convert 2000cm3 to L
2000cm3 = 2L
200
What is the Pythagoras Theorem formula?
c2 = a2 + b2
300
Are the following 2 triangles congruent? And what test will be applied to prove congruency?
Yes - SAS
300
Find the area of the following circle:
Area = ∏r2
A = ∏ x 102
A = 314.16
300
Calculate the area of the following composite shape:
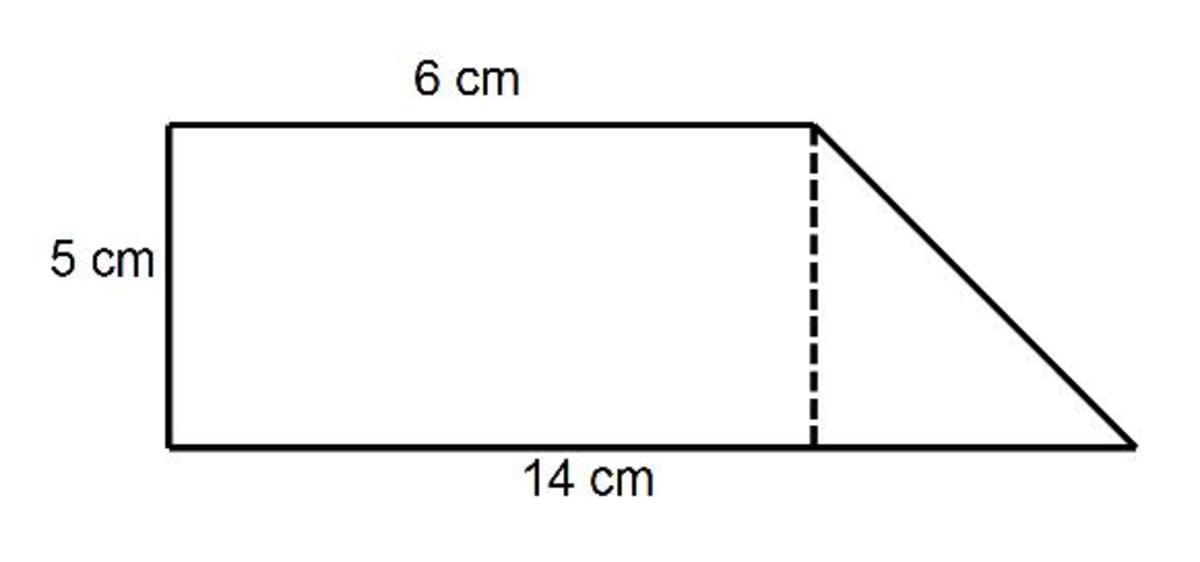
Rectangle: LxW
A = 5cm x 6cm = 30cm2
Area of Triangle = ½bh
A = ½ x 8cm x 5cm
A = 20cm2
Total Area = 30cm2 + 20cm2 = 50cm2
300
Find the volume of the following prism:
Volume = Area of face x height/length
V = ½bh x height
V = ½ x 9cm x 4cm x 12cm
V = 216cm3
300
Find the length of the hypotenuse:
a2 + b2 = c2
72 + 82 = c2
√72 + 82 = c
10.63 = c
400
These 2 triangles are similar. What is the scale factor, and what is the value of x.
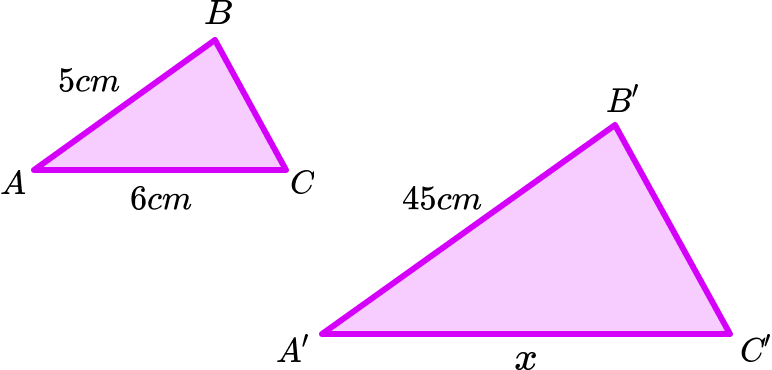
SF = 9 therefore x = 54cm
400
Find the area of the following shape:
Area of semi-circle = A of circle divide by 2
A = ∏r2/2
A = ∏ x 9cm x 9cm /2
A = 254.47cm2 /2
A = 127.24cm2
400
Calculate the perimeter and area of the following composite shape:
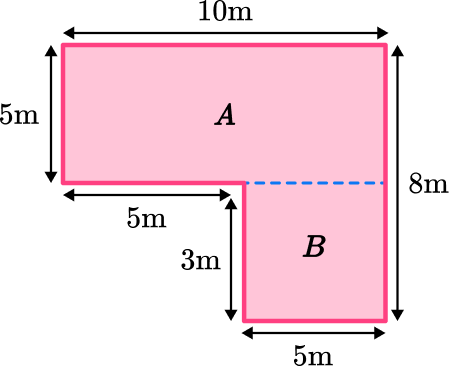
Perimeter = sum of all sides
P = 10m + 8m + 5m + 3m + 5m + 5m = 36m
Area of A = L x W
A = 5m x 10m = 50m
Area of B = L x W
A = 3m x 5m = 15m
Area of Composite Shape = Area A + Area B
A = 50m + 15m = 65m2
400
Find the volume of the following cylinder:
Volume = Area of face x height/length
V = ∏r2 x height
V = ∏x72 x 10cm
V = 1539cm3
400
Francis saw a ladder leaning on a 10m wall. If the ladder was 5m away from the wall, how long will the ladder be?
A diagram may help...
a2 + b2 = c2
5m2 + 10m2 = c2
√52 + 102 = c
11.18m
The ladder is 11.18m long
500
These 2 triangles are similar. What is the scale factor, and what is the value of x.
SF = 3 therefore x = 18cm
500
Calculate the area of the following composite shape:
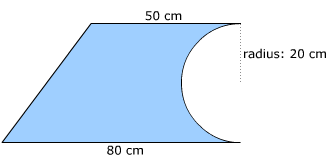
3 shapes: 1. Triangle, 2. Rectangle, 3. Semi-Circle
Area of Triangle = ½bh
A = ½ x 30cm x 40cm = 600cm2
Area of Rectangle = L x W
A = 50cm x 40cm = 2000cm2
Area of Semi-circle = ∏r2/2
A = ∏ x 202 /2 = 628.32cm2
Area of Composite Shape: 1 + 2 - 3
A = 600cm2 + 2000cm2 - 628.32cm2 = 1971.68cm2
500
Find the area of the following composite shape:
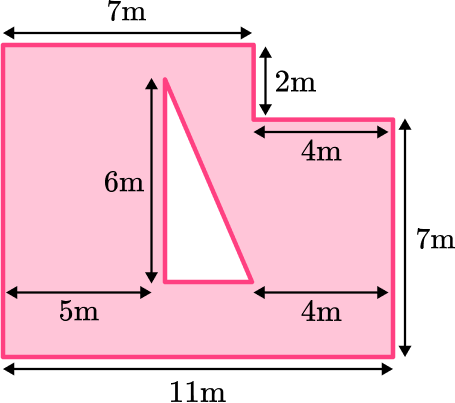
A = 85m2
500
Express the capacity of the following prism in Litres (l)
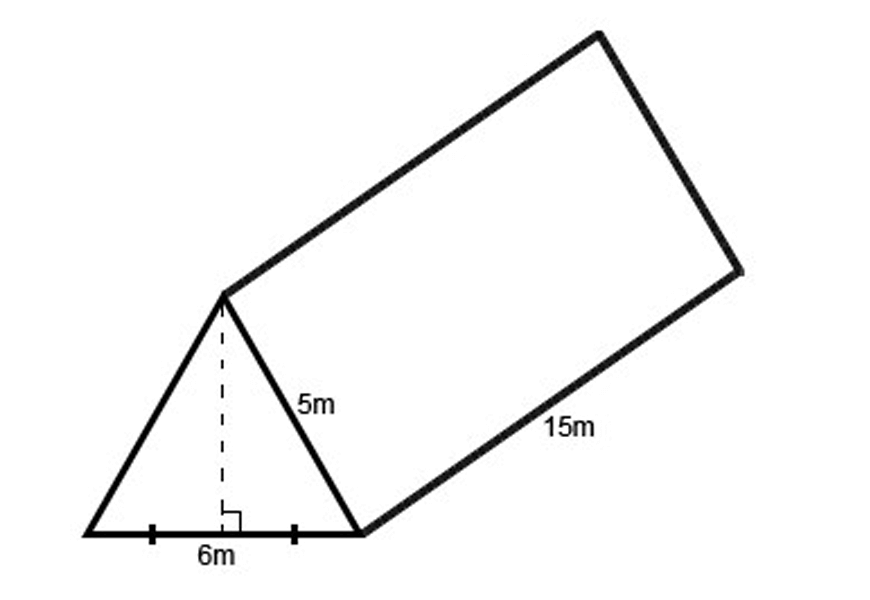
1m3 = 1000L
Therefore - 3 x 5 x 15 x 1000 = 225,000L
500
There are 2 buildings 20 metres apart. 1 building is 25m taller than the other. If you were standing at the top of the taller building, how far would you need to jump, if you wanted to land on the roof of the smaller building?
A diagram may help...
(WARNING: Please don't try this - theoretically only!)
a2 + b2 = c2
20m2 + 25m2 = c2
√202 + 252 = c
32.02m
You will need to jump 32.02m long (LOL)