Propositional Logic
(U1)
(U1)
Sets, Functions, Relations
(U2)
(U2)
Counting & Probability
(U3)
(U3)
Graph Theory & Number Theory
(U2, U4)
(U2, U4)
Mystery
100
Given the truth table below, evaluate the truth value of: \forall x \exists y F(x,y)
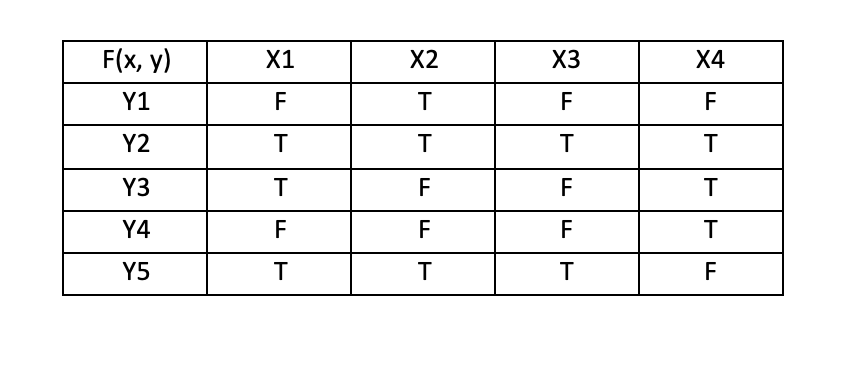
True
100
Which of the following sets is a family?
(A) { {a, e}, b, c, d}
(B) { a, b, c, d, e }
(C) {{}, {a}, {b}, c }
(D) {{a, b}, {b, c}, {c, a}}
(D) {{a, b}, {b, c}, {c, a}}
100
A girl scout troop with 10 girls and 2 leaders goes on a hike. When the path narrows they must walk in a single file line with a leader at the front and back of the line. How many ways are there for the entire troop (scouts and leaders) to line up?
2! 10!
100
Given this postfix expression, determine the original expression (in infix). Note: x and y are variables, * + - ÷ are operators.
3 5 x * + 10 x y ÷ - * y +
(5x+3)(10 - x/y) +y
100
Sort this set S into equivalence classes mod 7. S = {2, 18, 23, 35, 41, 48, 50, 66, 87, 92}.
[0] = {35}
[1] = {50, 92}
[2] = {2, 23}
[3] = {66, 87}
[4] = {18}
[5] ={}
[6] = {41, 48}
200
State the converse of: If I study, I will do well on the exam.
Is the converse equivalent to the original statement?
If I do well on the exam, then I studied. No, it is not equivalent.
200
Is the function f: R \to R , f(x) = -x^3 +4 onto? One-to-one? A bijectiion?
If it is a bijection, find it's inverse.
It is a bijection, and it's inverse is
f^-1(x)= root(3)(4-x).
200
A club is placing an order for shirts for its members. There are 12 members and each will get one shirt. The club is getting the shirt from a store that has 30 types of shirts. How many different shirt orders are there?
( (12 + 30 -1), (30-1))
200
Draw a complete graph on 6 vertices. What is its vertex-connectivity? What is its edge-connectivity?
It is 5-vertex connected and 5-edge connected.
200
State the logical negation of: Some people use computers, but cannot code.
Everyone either doesn't use a computer, or can code (or both).
300
Use a truth table to determine if the expression is a tautology, contradiction, or neither: (p \implies q) \iff (p ∧ ¬ q)
Contradiction
300
Given the graph G, would there be an edge from vertex a to vertex in G^3
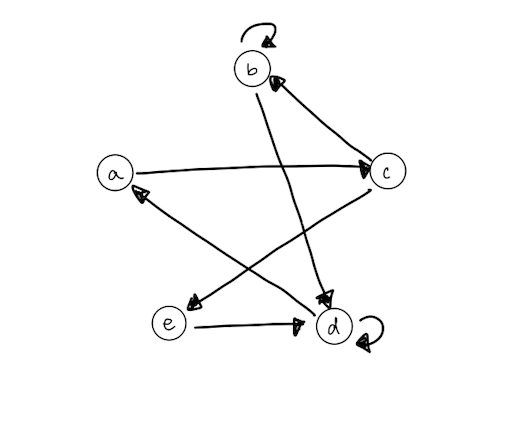
No, there's no path of length three from a to e in G.
300
There are 20 distinct candies in a bag, and a tutor wants to know the number of ways she could possibly to distribute the candy to her 6 students. All the candies must be given out, but there's no limitation to how many a single student receives. How many ways can she distribute the candy?
6^20
300
The following parameters are chosen to generate the public and private keys for the RSA cryptosystem.
p = 17 q = 11 e = 131 d = 11
If the ciphertext is c = 5, how would you calculate the plaintext m ?
Bonus: Simplify it to get m!
N = 187, m = cd mod N
m = (5)11 mod 187
= 181 (Bonus!)
300
Which of the following complete bipartite graphs have a Hamilton Cycle?
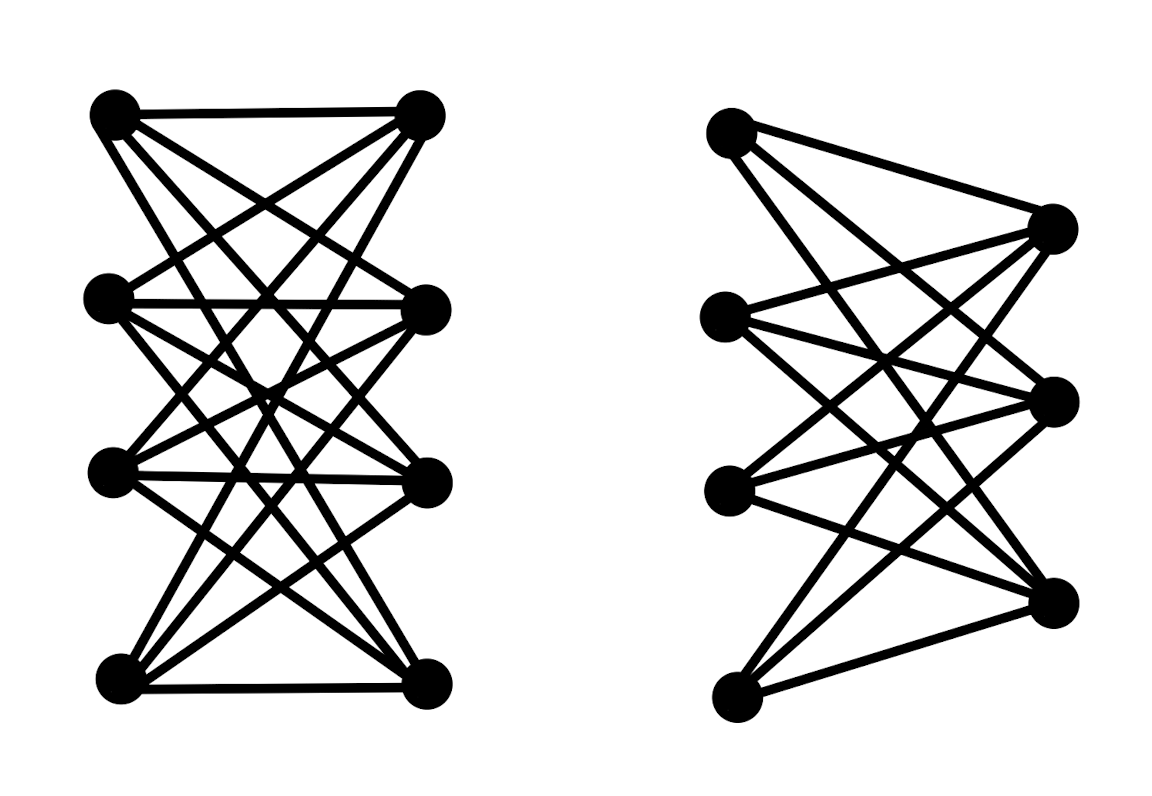
The K4,4 on the right.
400
Prove that the argument is valid using rules of inference:
j ∨ ¬ s
s ∨ h
\implies j ∨ h
1) j ∨ ¬ s (premise)
2) s ∨ h (premise)
3) ¬ s ∨ j (identity, 2)
4) h ∨ j (resolution)
5) j ∨ h (identity, 4)
400
Find the algebraic form of the sequence: 110, 60, 10, -40, -90, ... for domain i = 1, 2, 3, ...
a_k = 110 - (k-1)50
400
In a special lottery game, a player rolls three dice. One is a weighted dice where the probability of rolling a 1 is twice as likely as any other outcome. The player wins if they roll 3 sixes, what is the probability of winning?
(1/6)(1/6)(1/7)
400
Use Kruskal's Algorithm to find a minimum spanning tree of the following graph.
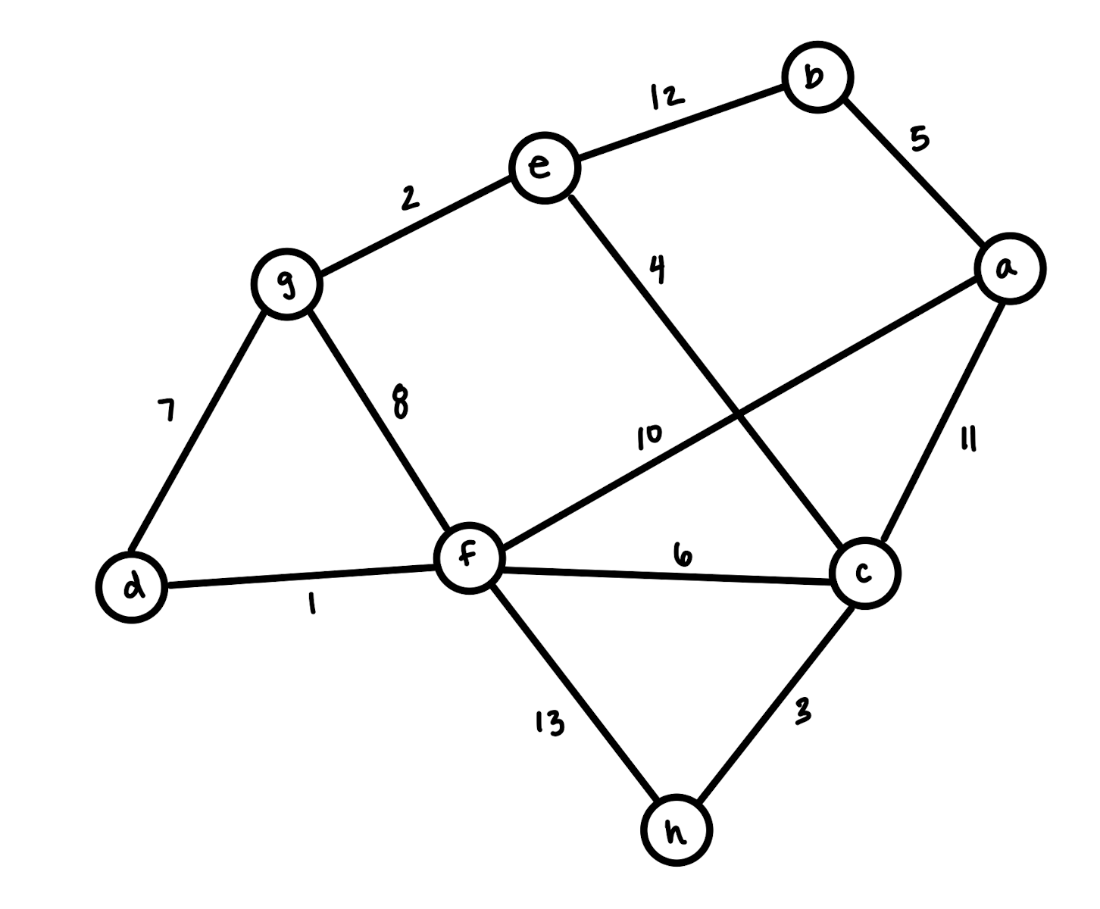What is the weight of that tree?
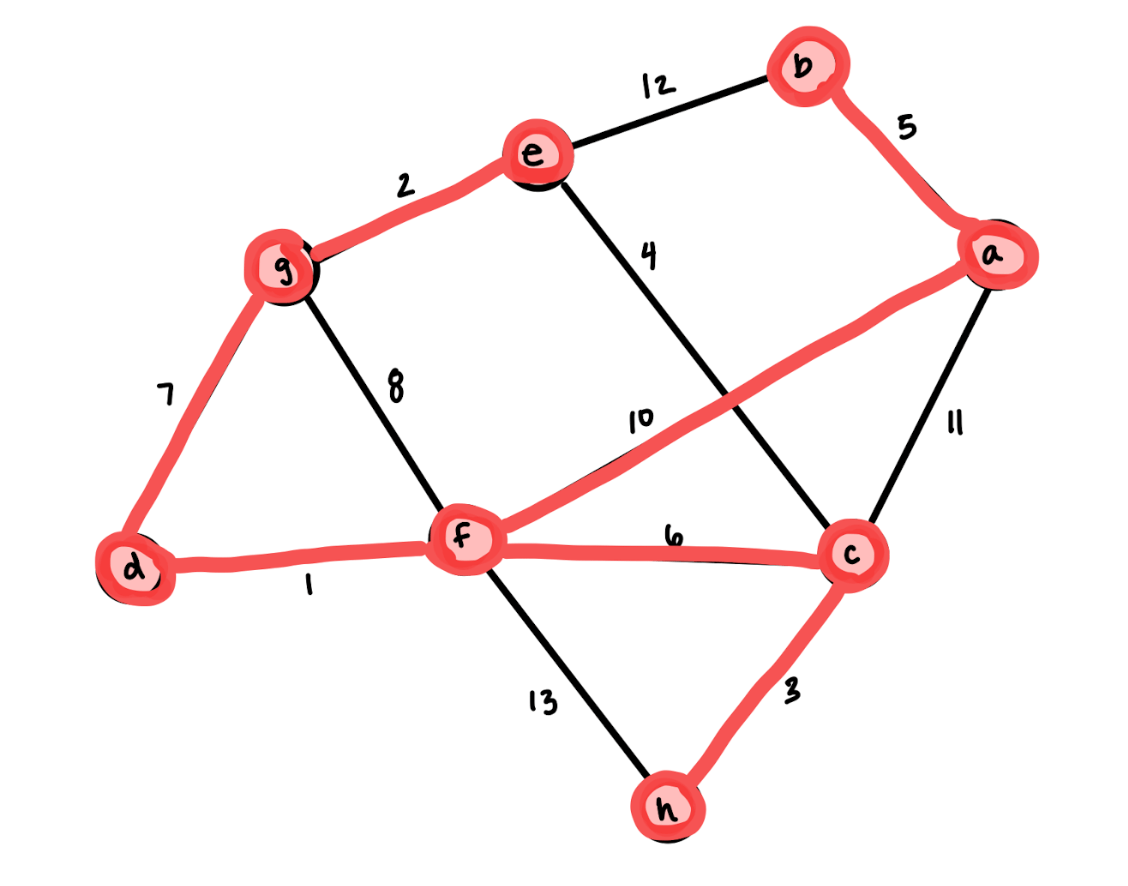
Total weight: 34
400
Count the number of strings of length 9 over the alphabet {a, b, c} that have exactly two a's, exactly, two b's, or exactly two c's.
|A \cup B \cup C| = |A| +|B|+|C| - |A cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C|
= ((9), (2))2^7 + ((9), (2))2^7 + ((9), (2))2^7 - ((9), (2))((7), (2))- ((9), (2))((7), (2))- ((9), (2))((7), (2)) +0
= 3(((9), (2))2^7) - 3(((9), (2))((7), (2)))
500
Use contradiction to prove that 2 - sqrt2 is irrational.
Assume that
2- sqrt 2
is rational. Then
2 - sqrt 2 = x/y
, where x and y are integers and y ≠ 0. Add 2 to both sides of the equation to get
2= x/y + sqrt 2
. Subtract
x/y
from both sides of the equation to get
2−x/y= sqrt 2
. The expression
2−x/y
is equal to
(2y−x)/y
. Therefore
sqrt 2=(2y−x)/y
. Since x and y are both integers, 2y-x is also an integer. Furthermore, y is a non-zero integer. Since 2 is equal to the ratio of two integers in which the denominator is non-zero, then we have shown that 2 is rational, contradicting the fact proved earlier that
sqrt 2
is irrational. Therefore the assumption that
2 - sqrt 2
is rational is false and therefore
2 - sqrt 2
must be irrational.
500
The following matrix represents a relation. Use it to draw a digraph representing the relation and then find the transitive closure of the graph.
[ [1, 1, 0, 1], [0, 1, 0, 0], [1, 1, 0, 0],[0, 1, 0, 1]]
The graph and its transitive closure are the same.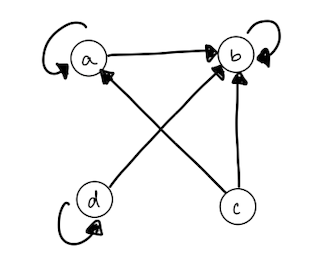 
500
A fair coin is tossed three times. Let Y be the random variable that denotes the square of the number of heads. For example, in the outcome HTH, there are two heads and Y = 4. What is the expected value of Y?
E[Y] = 0·(1/8) + 1·(3/8) + 4·(3/8) + 9·(1/8) = 24/8 = 3.
500
You're creating an RSA public and private key. You've chosen the primes p = 23 and q = 31, and you've chosen e = 59. What is your private key d?
d is the multiplicative inverse of e mod Phi = (p-1)(q-1)
d = 179
500
Define the sequence {bn} as follows:
- b0 = 1
- bn = 2bn-1 + 1 for n ≥ 1
Prove using induction that for n ≥ 0, bn = 2n+1 - 1.
By induction on n.
Base case: n=0
b_0 = 2^{0+1} -1 = 1
as defined.
Inductive step: Assume that
b_k = 2^{k+1} -1.
Consider b_{k+1} .
b_{k+1} = 2b_k +1
= 2(2^{k+1}-1) +1
(by the induction hypothesis.)
= 2*2^{k+1} -2 +1
= 2^{k+2} -1.
■