Write an equation in slope intercept form that goes through the following two points?

y = 14x - 62
The state fair is a popular field trip destination. This year the senior class at High School A and the senior class at High School B both planned trips there. The senior class at High School A rented and filled 8 vans and 8 buses with 240 students. High School B rented and filled 4 vans and 1 bus with 54 students. Every van had the same number of students in it as did the buses. Define the variables and write the system that represents the situation.
v = vans
b = buses
8v + 8b = 240
4v + b = 54
What is the formula for Arithmetic Sequence?
an = a1 + d(n - 1)
sqrt6/sqrt7
sqrt42/7
Solve the following quadratic equation via factoring:
x^2-24x+144=0
x = 2
What is the solutions of the system?
y=x^2-4x+4
y=x-2
Solutions: Two Real Solutions
(2, 0) and (3, 1)
Write an equation of a line that is parallel to the following equation and point.
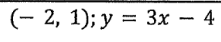
y = 3x + 7

Define the variables and write a system that represents the situation.
x = salad
y = lemonade
3s + 2l = 14
2s + 4l = 12
What is the formula for Geometric Sequence?
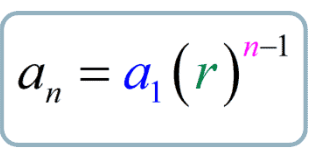
sqrt(24x^7) * sqrt(30x^6)
12x^6sqrt(5x)
Solve the following Quadratic Equation via factoring:
5x^2-19x=-18
t = 9/5 and t=2
What is the solution to the following system?
y=-(x+2)^2+5
y=5
One Real Solution: (-2, 5)
Write an equation of a line that is perpendicular to the following equation and point.
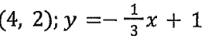
y = 3x - 10
Solve the following system of equations using either substitution or elimination.
3s + 2l = 14
2s + 4l = 12
s = 4
l = 1
What is the formula to find the sum of the terms in an Arithmetic Sequence?

3sqrt(18x) + 2sqrt(5x)
9sqrt(2x)+2sqrt(5x)
Solve the following equation via the quadratic equation:
2x^2+x=5
x= (-1+-sqrt41)/4
What is the solution to the the following system?
y=x^2-2x+4
y=x-1
No Solution
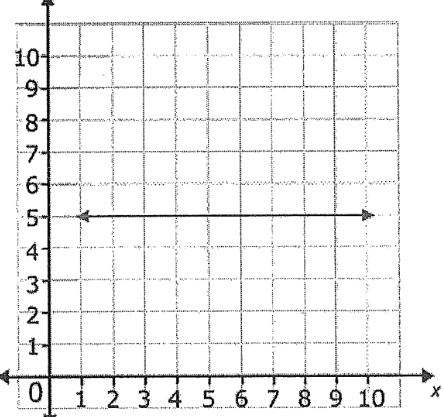
What is the slope of the following line.
The school that Stefan goes to is selling tickets to a choral performance. On the first day of ticket sales the school sold 3 senior citizen tickets and 1 child ticket for a total of $38. The school took in $52 on the second day by selling 3 senior citizen tickets and 2 child tickets. Define the variables and write the system.
Variables:
x = senior citizen
y = child
3x + y = 38
3x + 2y = 52
Firewood is stacked in a pile. The top row has 14 logs. There are 7 rows of logs. Each row has 2 more logs than the previous row. How many logs are there in all?
224 logs total
-4sqrt(28x) * sqrt(7x^3)
-56x^2
Solve the following Quadratic Equation using the Quadratic Formula:
5x^2+10x+7=0
No Solution
What is the solution to the following system?
y=-x^2+2x+7
y=-2x+2
Two Real Solutions:
(5, -8) and (-1, 4)
What is the slope of the following line?
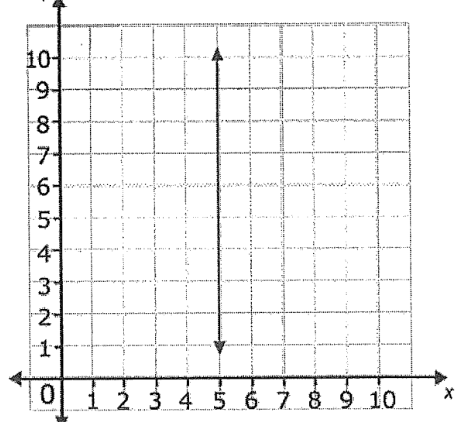
Undefined
The school that Stefan goes to is selling tickets to a choral performance. On the first day of ticket sales the school sold 3 senior citizen tickets and 1 child ticket for a total of $38. The school took in $52 on the second day by selling 3 senior citizen tickets and 2 child tickets. Solve the following system to figure out the cost of 1 senior citizen ticket and 1 child ticket.
3x + y = 38
3x + 2y = 52
senior citizen ticket: $8
child ticket: $14
Find the 12th number in the Geometric Sequence: 16, 12, 9, 27/4
*Make sure you leave your final answer as a simplified fraction.
177147/262144
sqrt(18a^3) * 4sqrt(3a^2)
12a^2sqrt6
Use either factoring or the Quadratic Formula to solve the following Quadratic Equation.
4y^2-4y-3=0
x=-1/2 and x=3/2
The path of a firework is described by the function:
h(t)=-4.9(t-5)^2+124
where h(t) is the height of the firework, in meters, and t is the time in seconds since launch.
a. What is the maximum height of the firework?
b. How many seconds does it take for the firework to reach the maximum height?
c. Use the quadratic formula to solve for how long the firework is in the air. (Round final answer to the nearest unit.)
a. 124 meters
b. 5 seconds
c. 10 seconds