Deg, Shape, End Beh.
Zeroes
Extrema
Increase/Decrease
Applications
100
Degree of f(x)=7x4+2x3-5x+9.
What is 4?
100
They are the zeroes of the table below.
x -2 -1 0 1 2 3 4 5
y -18 0 4 0 -6 -8 0 24
What are -1, 1, and 4?
100
According to the table this is the absolute maximum of this function.
x 1 2 3 4 5 6 7 8
y -24 0 -8 -12 0 16 0 -108
What is (6, 16)?
100
According to the table, the graph of the polynomial function is doing this on the interval x<-1
x -2 -1 0 1 2 3 4 5
y 8 3 0 -1 0 3 8 15
What is decreasing?
100
If two values are separated by 8 units, then their product is P(x)=x2+8x. This is the least product those values can possibly have.
What is -16?
200
It is the minimum possible degree of a polynomial graph that has 5 extrema.
What is 6?
200
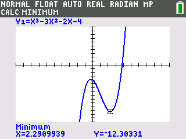The real zero for this function is closest to this integer.
What is 4?
200
According to the table, the ordered pair (0, -8) would be classified as this.
x -2 -1 0 1 2 3 4 5 6
y 24 0 -8 -6 0 4 0 -18 -56
What is a relative minimum?
200
According to the table, this is the x-interval for which this function is decreasing.
x -2 -1 0 1 2 3 4 5
y -18 0 4 0 -6 -8 0 24
What is 0<x<3?
200
A store's profit on sunglasses sold in thousands of dollars is modeled by P(x)=-x2+30x-12 where x is the cost of a pair of sunglasses. This is the price that would maximize the store's profit.
What is $15.00
300
It is the end behavior of this function.
As x -> 00, f(x) -> 00 and as x -> -00, f(x) -> -00
300
Based on the following table the zeroes of the function are located in these integer intervals.
x -4 -3 -2 -1 0 1 2 3
y 155 52 -21 -64 -77 -60 -13 64
What are -3<x<-2 and 2<x<3
300
It is the absolute maximum of f(x)=-4x2+6x-3.
What is (0.75, -0.75)?
300
This is what the function f(x)=x2+2x-8 is doing for the interval x>-1.
What is increasing?
300
A store's profit on sunglasses sold in thousands of dollars is modeled by P(x)=-x2+30x-12 where x is the cost of a pair of sunglasses. This is the maximum profit they can earn.
What is $213,000
400
It is the leading coefficient of f(x)=2x7-5x3-8x9+1.
What is -8?
400
They are the zeroes of f(x)=3x2-8x-3. Round if necessary.
What are x=-1/3 and x=-3?
400
This would be the classification of (2, -9) in the function f(x)=-x3+10x2-28x+15.
What is a relative minimum?
400
This is the interval for which the function f(x)=x3+2x2-8x-2 is decreasing. Round to the nearest tenth.
What is -2.4<x<1.1?
400
A welder is going to create a box without a lid by cutting a square out of each corner of a rectangular piece of sheet metal with dimensions of 90 cm x 60 cm and folding up the flaps to weld the edges of the box. If x represents the side length of the square he cuts out, this would be the formula for volume in terms of x.
What is V(x)=x(90-2x)(60-2x)
or
V(x)=4x3-300x2+5400x?
500
It is the maximum number of turning points for a polynomial of nth degree.
What is n-1?
500
It is the maximum number of real zeroes in an nth degree polynomial.
What is n?
500
The product of two consecutive odd integers can be represented by P(x)=4x2 -1. This is the minimum possible product of two consecutive odd integers.
What is -1?
500
This is the term for a function that increases over its whole domain (or decreases over its whole domain).
What is monotonic?
500
A company knows that if they sell baseball bats for $30, they will sell 850 bats. For every dollar they increase the price, they will sell 5 fewer bats. Let x be the number of $1 increases that the company raises the price of their bats. This is the formula for their profit in terms of x.
What is P(x)=(-5x+1000)(x+30)
or
P(x)=-5x2+850x+30000?