Find the interval where f(x) is concave up. Justify your answer.

f(x) is concave up on (1, 4) because the average rates of change are increasing.
What is the degree of the following function?
6x^7+3x^8-2x^2
8
What is the end behavior of the following function?
(4x^3+2x^2-7)/(5x^3+6)
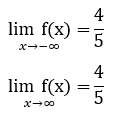
Let
f(x)=x^2+4x+1.
Write an equation of the following functions that are transformations of f(x).
g(x)=3f(x)-7
3x^2+12x-4
On what open intervals is k(x) both increasing and concave down? 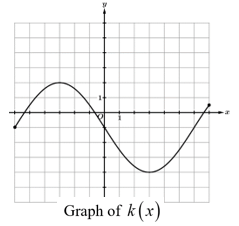
(-6,-3)
Where does f(x) have an inflection point? Justify your answer.

f(x) has an inflection point at x = 1 because the average rates of change change from decreasing to increasing at x = 1.
Use the limit definition to state the end behavior of the polynomial functions.
f(X)= -8x^7+3x^2+5
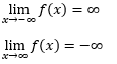
Find the horizontal asymptote of
(x^3+x^2-9)/(x^5-3x^2-5x)
y = 0

Selected values of the continuous function g(x) are shown in the table above. Use the values in the table to answer the following. Let
h(x)=-2g(x-3)-5.
Find h(0).
h(0) = 3
Calculate the average rate of change of the function 𝑓(𝑥) =
x^2-9x
in the interval 2 ≤ 𝑥 ≤ 7.
0
The table gives values of a function f for selected values of x. Is the function linear or quadratic? Justify your choice?

f(x) is quadratic; f(x) has a constant second difference over equal-length input value intervals OR the rates of change are changing at a constant rate.
Where is the relative maximum of the function? (Calc. okay)
h(x)=2x^3-4x
(-0.816, 2.177)
Find the zeros of the function.
(4-x^2)/(x-2)
-2
The graph of f(x) is shown in the figure below and has the domain [-3,3] and the range [-5,3].
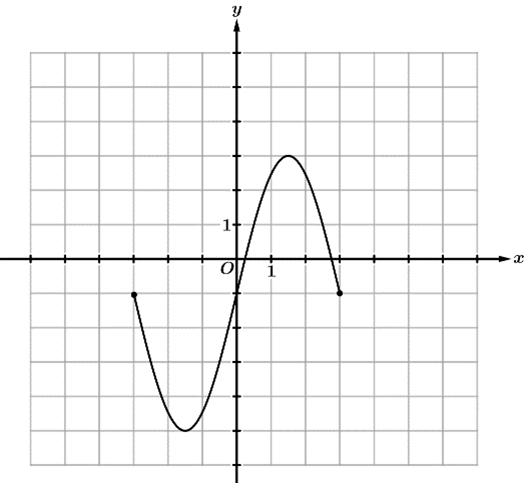
Let k(x)=-3f(2x)+1.
Find the domain and range of k(x).
Domain
[-3/2,3/2]
Range [-8,16]
Let g be an odd function that is strictly increasing. Selected values of g(x) are given in the table above. Find the values of the constants a, b, and c.
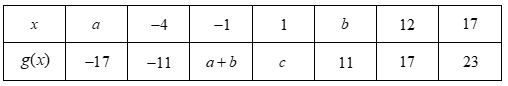
a = -12
b = 4
c = 8
Let
f(x)=x^2-4
The average rate of change of over the interval [c, 5] is equal to 3, where c is a constant. Find the value of c.
c = -2
Given the zero 4 − 𝑖, find all other zeros of the polynomial function
f(x)=x^4-8x^3+16x^2+8x-17
−1, 1, 4 − 𝑖, 4 + i
Find the zeros, vertical asymptote and holes if any.
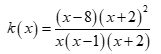
zero x = 8 (8, 0)
VA x = 0, x = 1
Hole x = -2

Selected values of the continuous function h(x) are shown in the table above. Use the values in the table to answer the following. Let
h(x)=6f(x+2)-3
Find f(4).
f(4) = 0
Find the line of best fit of the percentage of American homeowners.

regression equation: _______
regression equation
-0.009786x^2+38.7647x-38325.5
Let p(x) be the function that results from applying three transformations to the graph of g in the order: a horizontal dilation by a factor of 1/2, a reflection over the y-axis, and a vertical translation by 1 unit.
Find the average rate of change of p over the interval [-1/2, 4].
g(x)=x^2-2
Which of the following statements are true about the polynomial function p(x)?
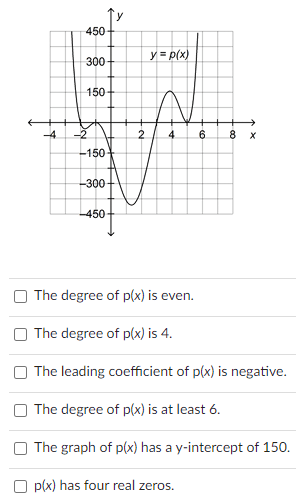
The degree of p(x) is even.
The degree of p(x) is at least 6.
p(x) has four real zeros.
Solve the following inequality. Answer using interval notation.
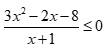
(-∞,4/3] ∪(-1,2]

Let
w(x)=2h(x-3)+1
Find w(w(2)).
w(w(2)) = 3
A sheet of 16 cm x 12 cm card is used to make an open box. Four identical squares are cut out of each corner. Then, the remaining card is folded to make an open box. For what value of x is the volume the largest?
x = 2.26