Understanding Fractions
+ and - Fractions
Equivalent Fractions
x and ÷ Fractions
Random
100
Convert to an improper fraction:
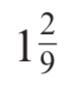
11 / 9
100
TRUE or FALSE
When + or - fractions, the denominators MUST be the same
TRUE
100
Fill in the gap
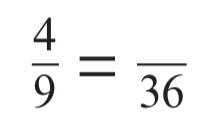
16/36
100
TRUE or FALSE
When x or ÷ fractions, the denominators MUST be the same
FALSE
100
The first 3 multiples of 3
3, 6, 9
200
Convert to an improper fraction: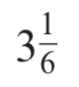 
19 / 6
200
Calculate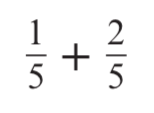 
3 / 5
200
Fill in the gap
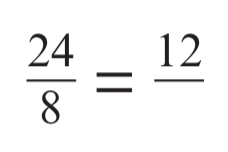
12/4
200
Calculate:
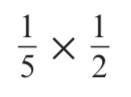
1 / 10
200
The first 4 multiples of 7
7, 14, 21, 28
300
Convert to a mixed number:
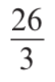
8 2/3
300
Explain how to get the denominators of two fractions the same
Find a common multiple of both denominators. What ever you do to the bottom of the fraction (x or ÷), you must also do to the top
300
Fill in the gap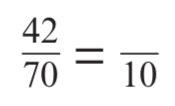 
6/10
300
Calculate: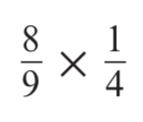 
2 / 9
300
The lowest common multiple of 6 and 12
12
400
Explain the difference between a proper fraction, improper fraction and mixed number
Proper fraction: numerator < denominator
Improper fraction: numerator > denominator
Mixed number: whole number and fraction
400
Calculate
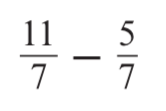
6/7
400
Explain equivalent fraction
A fraction that has the same value as the original fraction
400
Calculate: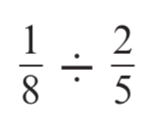 
5 / 16
400
The highest common factor of 12 and 16
4
500
There are 60 minutes in 1 hour. What fraction of an hour is 17 minutes?
17 / 60
500
Calculate
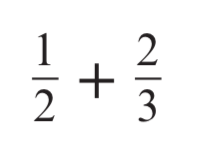
3/6 + 4/6
= 7/6
= 1 1/6
500
Fill in the gaps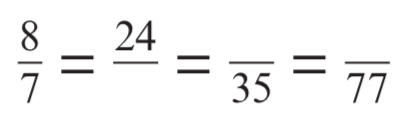 
24/21
40/35
88/77
500
Explain how to ÷ fractions
Step 1: Change the ÷ to a x
Step 2: Turn the second fraction into a reciprocal
Step 3: Proceed like a x problem (simplify vertically or horizontally, multiple the numerators, multiply the denominators, convert improper fractions to mixed numbers where possible)
500
List the factors of 48
1, 2, 3, 4, 6, 8, 12, 16, 24, 48