1.1-1.2
1.3-1.4
1.5-1.6
1.7
idk
100
f(x) = 2x - 2
g(x) = 7 - x2
Find f(-3) + g(2)
f(-3) = 2(-3) - 2 = -6 - 2 = -8
g(2) = 7 - (2)2 = 7 - 4 = 3
-8 + 3 = -5
100
solve the absolute value equation:
| x + 4 | = 18
x + 4 = 18 -(x + 4) = 18
x + 4 = 18 x + 4 = -18
x = 14 x = -22
100
Find the inverse of the following equation:
f(x) = x / x + 5
f(x) = x / x + 5
y = x / x + 5
switch x and y
x = y / y + 5
x * (y + 5) = y
xy + 5x = y
5x = y - xy
5x = y(1 - x)
5x / 1 - x = y
f-1(x) = 5x / 1 - x
100
Find the rate of change:
f(x) = 4x2 - 7 on [1, b]
f(b) - f(1) / b - 1
f(b) = 4b2 - 7
f(1) = 4(1)2 - 7 = -3
4b2 - 7 - (-3) / b - 1
4b2 - 4 / b - 1
4(b2 - 1) / b - 1
4(b + 1)(b - 1) / b - 1
= 4(b + 1)
100
Which method determines if a graph is a function
Vertical Line Test
200
Find the Domain and Range of the graph below
Domain: (-3, 1]
Range: [-4, 0]
200
f(x) = x2 + 6x
g(x) = 2 - x2
Find f(g(2))
g(2) = 2 - 22 = 2 - 4 = -2
f(-2) = (-2)2 + 6(-2)
= 4 - 12 = -8
200
Describe the transformation of this function:
f(x) = 4 * |x - 2| - 6
shift right 2 units
shift down 6 units
vertically stretched by a factor of 4
200
Find the average rate of change of the function f(x)=6−3x2 on [−2,3]
f(b)−f(a) / b−a
f(3) - f(-2) / 3 - -2
f(3) = 6 - 3(3)2 = 6 - 27 = -21
f(-2) = 6 - 3(-2)2 = 6 - 12 = -6
-21 - -6 / 3 - -2
-15 / 5 = -3
200
BONUS QUESTION:
A rain drop hitting a lake makes a circular ripple. If the radius, in inches, grows as a function of time in minutes according to r(t)=10√t+5, find the area of the ripple as a function of time
Area of a circle: A = pi * r2
radius: r(t)=10√(t+5)
A = pi * (10√t+5)2
A = pi * 100(t + 5)
300
What is the domain of the following:
f(x) = x2 + 2x + 1
All Real Numbers
300
If h(x) = f(g(x)) and h(x) = (x - 5)3
find f(x) and g(x)
g(x) = x - 5
f(x) = x3
300
given a function f(x) = x. Transform it to g(x) given the following:
horizontally compressed by 1/2
3 units to the left
shift up 1 unit
g(x) = 2(x + 3) + 1
300
Find the absolute max and/or min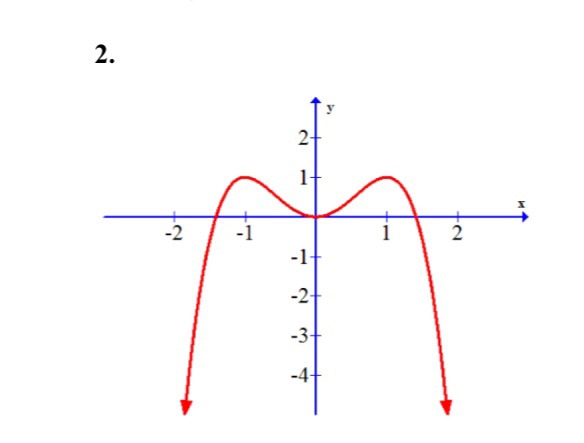
absolute max: 1 at x = -1, 1
absolute min: DNE
300
At the start of a trip, the odometer on a car read 21465. At the end of the trip, 13.5 hours later, the odometer read 22205. Assuming the scale on the odometer is in miles, what is the average speed the car traveled during the trip? Round to the nearest tenth of a mile.
x2−x1 / y2−y1
= 22205−21465 / 13.5−0
≈54.8 miles per hour
400
The quality of gasoline that a station sells in a day is a function of the price. Let Q = f(P) represent the number of gallons of gasoline the station sells in a day if it charges P dollars per gallon.
Interpret f(3.09) = 7840
When the station sells gasoline for $3.09, they will sell 7840 gallons in a day
400
f(x) = x2 + 6x
g(x) = 2 - x2
Find f(g(x))
f(g(x)) = f(2 - x2) = (2 - x2)2 + 6(2 - x2)
= 4 - 4x2 + x4 + 12 - 6x2
= x4 - 10x2 + 16
400
f(x)=2−x
find f-1(x)
f(x)=2−x Substitute y for f(x).
y=2−x Interchange the variables x and y.
x=2−y Solve for y.
y=2−x Substitute f-1(x) in for y.
f-1(x)=2−x
400
Find the interval of concave up, concave down, and the inflection point
(−∞,0), the function is concave down, while on the interval (0,∞), the function is concave up
inflection point: (0,1)
400
The price P charged by a taxi company for a trip x miles long is given by the formula
P = f(x) = 3.50 + 2.75x
The company will NOT make any trip longer than 50 miles.
Find the domain and range of this function
Domain: [0, 50] because the company will not go over 50 miles
Range: [3.50, 141]P = 3.50 + 2.75(50) = 141
500
Find the domain of this function:
8 / sqrt(x + 4)
x + 4 >= 0 (>= means greater than or equal to)
x >= -4
500
Solve the inequality
- | 1/3x - 3 | >= 17
(>= means greater than or equal to)
No Solution
Remember: The absolute value of a number n is written as | n | and | n | >= 0
- | 1/3x - 3 | >= 17
| 1/3x - 3 | <= -17
500
Describe the transformation given the following function:
f(x) = -(x + 2)2 - 1
reflected across the x-axis
left 2 units
down 1 unit
500
Let f(x)=1 / x. Find the number c such that the average rate of change of the function f on the interval (1,c) is −1/9
(1/c−1/1) / (c−1)= −1/9 Multiply both sides by (c−1) and 9.
9 * (1/c - 1) = 1 - c
9/c - 9 = 1 - c Multiply both sides by c.
9 - 9c = c - c2
c2 - 10c + 9 = 0 Factor
(c - 9)(c - 1) = 0
c = 1, c = 9
Since 1 is included in the interval, c = 9
500
