Key Features Expon. f(x)'s
Growth or Decay
Growth or Decay
Word Problems
Word Problems
100
If, y=a(bx ), What do a and b represent?
a=Starting point/y-intercept
b=growth factor
100
f(x)=a(.93)x
Does this functions represent exponential growth or decay? What is the percent growth/decay rate?
Exponential Decay
7% decay rate
100
A bunny population doubles every 6 months. If the starting population is 10, how many will you have after 3 years? What is the initial population? What is the growth factor?
initial population = 10
growth rate = 2
640 bunnies
100
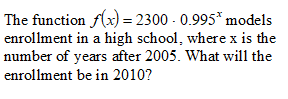
2243
100
A town has a population of 70,400 and decays at a rate of 4% every year. Write an equation represents the town’s population after x years?
y=70400(0.96)x
200
Which number is the y-intercept and which is the growth factor for the function f(x)=2(3)x
y-intercept=2
growth factor= 3
200
Find the equation for:
Passes through the points (0, 3.5) and (2, 31.5)
y=3.5(3)x
200
Annual sales of a fast food restaurant are $530,000 and increasing at a rate of 5%. What will the annual sales be in 6 years?
530,000(1.05)6 =$710,250.69
200
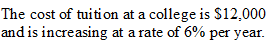
What will be the cost in 17 years?
$32,313.27
200
An element with mass 130 grams decays by 22% per minute. How much of the element is remaining after 7 minutes, to the nearest 10th of a gram?
22.8
300
What is the equation for the graph below?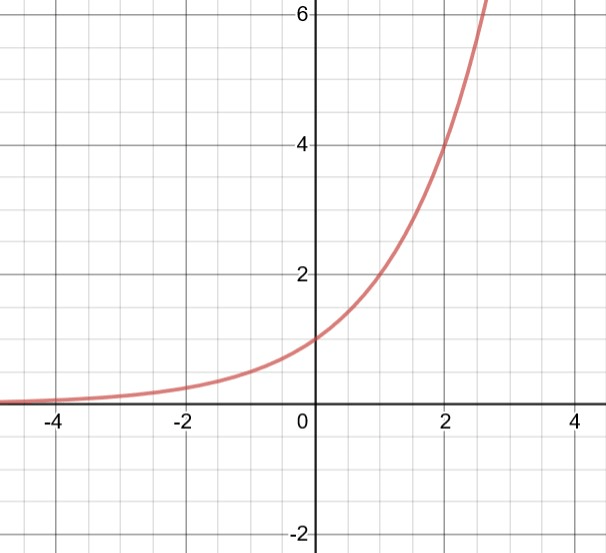
y = 2^x
300
Ms. Wiggins purchased a car for 26,400 and every year it decays by 12%. What can she expect the value of her car to be after 3.5 years?
f(x)=26400(.88)3.5=$16,876.92
300
The accompanying table shows the number of bacteria present in a certain culture over a 5 hour period, where x is the time, in hours, and y is the number of bacteria. Write an exponential regression equation for this set of data, rounding all coefficients to the nearest hundredth. Using this equation, determine the number of bacteria present after 11 hours, to the nearest whole number.
hours: 0 1 2 3 4 5
bacteria: 1800 1950 2154 2424 2730 3034
y=1768.43(1.11)x
5574
300
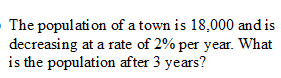
16,941 people
300
A town has a population of 13000 and grows at 4.5% every year. What will be the population after 13 years, to the nearest whole number?
23039
400
What's the growth factor?
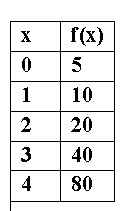
b=2
400
The accompanying table shows the value of a car over time that was purchased for 15400 dollars, where x is years and y is the value of the car in dollars. Write an exponential regression equation for this set of data, rounding all coefficients to the nearest hundredth. Using this equation, determine the value of the car, to the nearest cent, after 10 years.
years: 0 1 2 3 4
value: 15,400 13,409 11,881 10,056 8,975
y=15411.14(0.87)x
3828.49
400
The accompanying table shows the number of bacteria present in a certain culture over a 4 hour period, where x is the time, in hours, and y is the number of bacteria. Write an exponential regression equation for this set of data, rounding all coefficients to the nearest hundredth. Using this equation, determine the number of bacteria present after 10 hours, to the nearest whole number.
hours: 0 1 2 3 4
bacteria: 96 106 131 151 189
y=92.82(1.19)x
529
400
Is the function exponential growth or decay?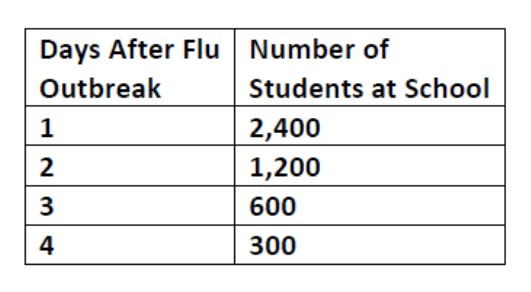 
Decay
400
Write an exponential function in the form y=abx that goes through the points (0,16) and (3,2000).
y=16(5)x
500
What is the rate? Is it a growth or decay?
y=204(0.0025)x
Decay
99.75%
500
The accompanying table shows the value of a car over time that was purchased for 18000 dollars, where x is years and y is the value of the car in dollars. Write an exponential regression equation for this set of data, rounding all coefficients to the nearest hundredth. Using this equation, determine the value of the car, to the nearest cent, after 13 years.
years: 0 1 2 3 4 5
value: 18,000 15,026 12,702 10,680 8,483 7,082
y=18217.12(0.83)x
1616.20
500
The accompanying table shows the number of bacteria present in a certain culture over a 4 hour period, where x is the time, in hours, and y is the number of bacteria. Write an exponential regression equation for this set of data, rounding all coefficients to the nearest thousandth. Using this equation, determine the number of bacteria present after 16 hours, to the nearest whole number.
hours: 0 1 2 3 4
bacteria: 279 310 343 382 457
y=274.779(1.127)x
1861
500
If you put $500.00 into an account and the account earns 3% interest, compounded quarterly. How much will be in the account after 5 years?
$580.59
500
Find the equation of the exponential function represented by the table:
x: 0 1 2 3
y: 0.1 0.05 0.025 0.0125
y=0.1(0.5)x