Random Skills
Similarity
Cross Multiplication
Trig
Applying Trig
100
Simplify:
\frac{a^2*c^3*d}{8acd^2}
Given:
a=2, c=3, d=4
9/16
100
Define similarity
When two (or more) shapes have corresponding sides that have been scaled consistently with some scale factor.
100
Cross multiply the following:
\frac{10}{x}=\frac{25}{6}
x=2.4
100
Which trig function takes opposite/hypotenuse?
\sin(\theta)
100
Explain how trig can be used to find the height of something
Answers vary
200
Write an equation of a line parallel to:
2x-8y=16
Any line with slope 1/4
200
Determine the scale factor given the following proportions of corresponding sides:
\frac{16}{5}=\frac{25.6}{8}=\frac{32}{10}
scale factor is 3.2
200
Explain why we can switch terms on the diagonals of proportions:
\frac{a}{b}=\frac{c}{d}
equal to:
\frac{d}{b}=\frac{c}{a}
When you cross multiply, a*d=b*c is still the result.
200
Explain why
\sin(\theta)<1
always
Because the hypotenuse will always be bigger than opposite. And so we have it that we're always dividing by a larger number. Can't be bigger than 1 (or even equal)
200
Suppose you have a 12 ft ladder propped up against a wall with an angle (on the ground) of 35°. How far up the wall does the ladder reach?
About 7 feet (6.88)
300
A:{2,4,6,7,8,10}, P:{2,3,5,7,}, U:{1-10}
What is
A \cap P
A \cap P:{2,7}
300
What is the scale factor relationship between Triangle A and Triangle C?
5\triangle A=\triangle B, 3\triangle B=\triangle C
15\triangle A=\triangle C
300
Solve for x
\frac{8}{3x-2}=\frac{12}{15}
x=4
300
Explain why
\tan(\theta)>1
is a possibility
Because, opposite may be much larger than adjacent, producing a fraction like
\frac{8}{3}=2.\overline{6}
300
Suppose you have a 12 ft ladder propped up against a wall with an angle (on the ground) of 35°. Explain why the height the ladder reaches will never be >12. (Even if you change the angle!!)
because the hypotenuse will always be the largest side!
400
Assume P(A) and P(B) are independent
if P(A)=0.85, P(B)=0.2 \text{ what is} P(A\cap B)
P(A\cap B)=0.17
400
Triangle A has a base of 4 and a height of 3. That makes the area 6. If we double the side lengths, how much does the area change? Show using the formula: A=(1/2)bh
4 times.
400
Keefe sets up a proportion, cross multiplies, and gets the following result.
1296=1340
What can Keefe conclude?
The two figures are NOT similar
400
Find theta if:
\sin(\theta)=10/11
\sin^{-1}(\frac{10}{11})\approx 65°
400
Given the following triangle, find the area:
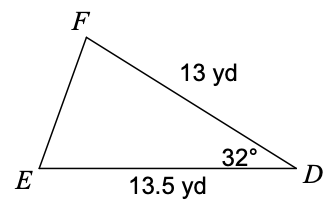
\approx 46.5
500
Write a quadratic equation with the following points:
(3,0),(-4,0), (0,-12)
f(x)=x^2+x-12
500
Triangle A has a base of 4, a height of 3 and a hypotenuse of 5. The perimeter is given by adding up all the sides. If we scale the triangle by 5, what is the new perimeter? How does the perimeter change with scale factor?
New perimeter is 5(3)+5(4)+5(5)=5(3+4+5)=5(12).
500
Solve for x
\frac{6}{5x+6}=\frac{3}{x-3}
x=-4
500
Which angle satisfies the following equation?
\sin(20°)=cos(\theta)
cos(70°)
500
Find the length of ED given that the area is: 83.2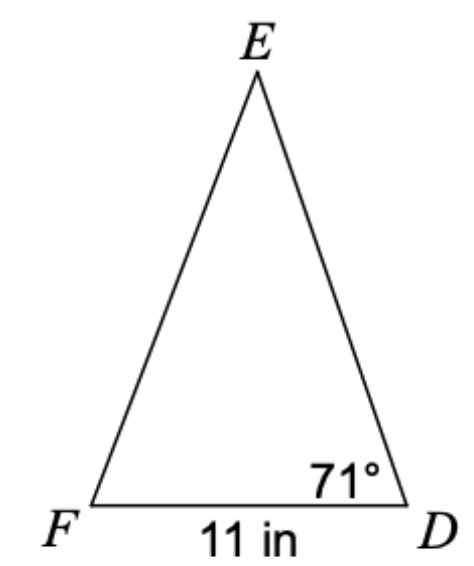
16