The name of the line that cuts the parallel lines.
What is a transversal?
The first reason on any algebra proof is this ____.
What is given?
Point a is in between point C and point B. Point C and point B are collinear. Therefore CA + AB = AC. This is an example of which postulate?
What is segment addition postulate
The following is an example of this property:
m/_1 = 150^o
m/_1 + m/_2 = 180^o
150^o + m/_2 = 180^o
What is substitution?
Write the statement as a conditional statement: All students love geometry
What is, if you are a student, then you love geometry?
Supplementary Angles add up to this many degrees.
What is 180°?
An example of angles that are on the same side of the transversal and are congruent.
What are corresponding angles?
It's the property used here:
x + 8 = 58
x = 50
What is the subtraction property of equality?
Give an example of the segment addition postulate, with a drawing. (Use the points A, B, and C).

AB + BC = AC
What is the slope for the line that is perpendicular to the following:
y = 3x +2
What is -1/3?
What is the hypothesis of the statement...
If the students study, then they will get a good grade on the next test.
What is, the students study?
Through 3 noncollinear points there is exactly one________
Plane
An example of angles that are on the same side of the transversal and are supplementary.
What is a linear pair, or same side interior/exterior?
This would be an example of the which property?
If /_A+/_B=180° and /_B+/_C=180°
then
/_A=/_C
Transitive
True/False. Definition of congruence is only used with segment proofs.
False.
How would you graph the line that is perpendicular to y = 2x + 6 and passes through (3,2)?
Determine the slope of the line that is perpendicular, use that slope(rise/run) from the point (3,2) to get to the new point. Graph the line between the two points.
(3,2) move down 1 over 2, this would be at (5,1)
What is the conclusion in the statement...
If you live in Saint Joseph, then you live in Missouri
What is, you live in Missouri?
A pair of opposite angles made by two intersecting lines that are congruent.
What are vertical angles?
An example of angles that are on opposite sides of the transversal and are congruent.
What are alternate interior/exterior or vertical angles?
It's the last reason for the following algebra proof:

What is the division property of equality?
This reason justifies statement 2 in the following proof.

What is the definition of midpoint?
This theorem tells us that
If
/_1 and /_2 are supplements
and /_2 and /_3
are supplements.
Then
/_1 cong/_3
What is the congruent supplements theorem?
What is the contrapositive of the following statement
If a number is prime, then it is odd.
What is, If a number is not odd (even), then it is not prime.
Two angles that are next to one another, have a common side, a common vertex, and don't overlap.
What are Adjacent Angles?
The Perpendicular Transversal Theorem states this.
What is: in a plane, if a line is perpendicular to one of two parallel lines, then it is perpendicular to the other?
It is a logical 2nd statement (assuming the first is a given):
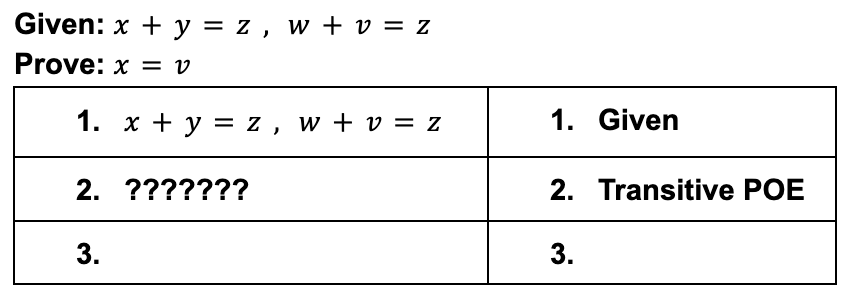
What is x + y = w + v?
It would be the last reason in the following proof:

What is the definition of segment congruence?
Give statement #6
What is
m/_1 + m/_5 = 180^o?
This is the statement that you use to connect a conditional with its converse to make a biconditional.
What is If and only if?
Write a conclusion and identify which law is used below for the two conditional statements:
If a students studies for 2 hours, then the student gets and A.
If the student gets and A, then their parents will be happy.
What is law of syllogism
If a student studies for 2 hours, then their parents will be happy.