Find the domain of the INVERSE of the following graph
[0, oo)
Find the domain and range of the INVERSE
f(x)=x^3 -5
Domain:
(-oo,oo)
Range:
(-oo,oo)
What restriction could be placed on the domain to make the inverse a function?
[0,oo)
Find the average rate of change.
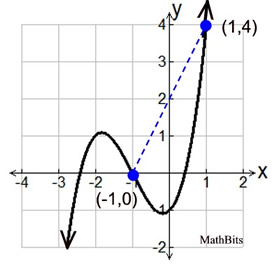
4/2=2
Find the inverse of the set of points.
(0,0) (-2,7) (5,15)
(0,0) (7,-2) (15,5)
Find the vertex of the INVERSE function.
f(x)=(x-4)^2 +5
(5,4)
Find the point of symmetry.
f(x)=(x-1)^3-2
(1,-2)
What restriction could be placed on the domain to make the inverse a function?
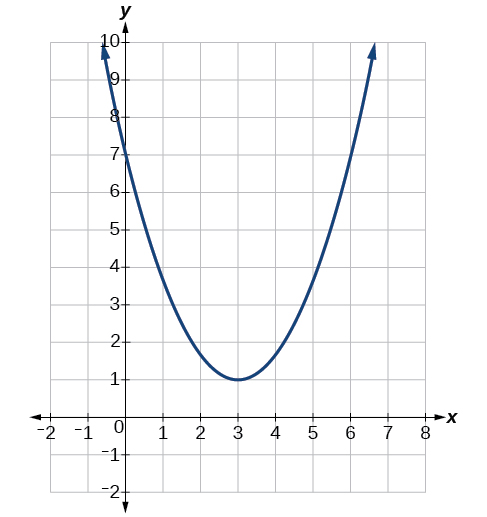
[3,oo)
Find the average rate of change.
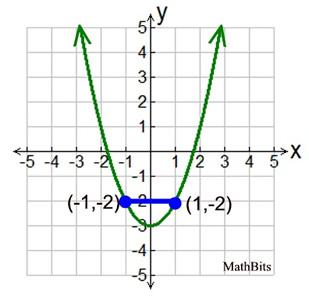
0/2=0
Find the inverse equation from the original algorithm.
Starting with a number,
Add 3
Take the cube root
Multiply the quantity by 4
Divide 4
Cube
Subtract 3
f^-1(x)=(x/4)^3-3
Find the domain and range of the graph.

Domain:
(-oo,oo)
Range:
[1,oo)
Determine the intervals of increasing and decreasing.
f(x)=-3x^3
Increasing: never
Decreasing:
(-oo,oo)
What restriction could be placed on the domain to make the inverse a function?
f(x)=(x+4)^2-2
[-4,oo)
Find the average rate of change.
(-3,5) and (4,9)
(9-5)/(4--3)=4/7
Find the inverse equation from the original algorithm.
Starting with a number,
Double the number
Square the quantity
Subtract 7 from the result
Add 7
Square root
Divide 2
f^-1(x)=sqrt(x+7)/2
Find the equation of the inverse function.
f(x)=-x^2-3
y=-x^2-3
x=-y^2-3
x+3=-y^2
-x-3=y^2
f^-1(x)=sqrt(-x-3)
Find the equation of the inverse.
f(x)=-5x^3+6
y=-5x^3+6
x=-5y^3+6
x-6=-5y^3
(x-6)/-5=y^3
f^-1(x)=root(3)((x-6)/-5)
What type of restriction would result in the following inverse graph?
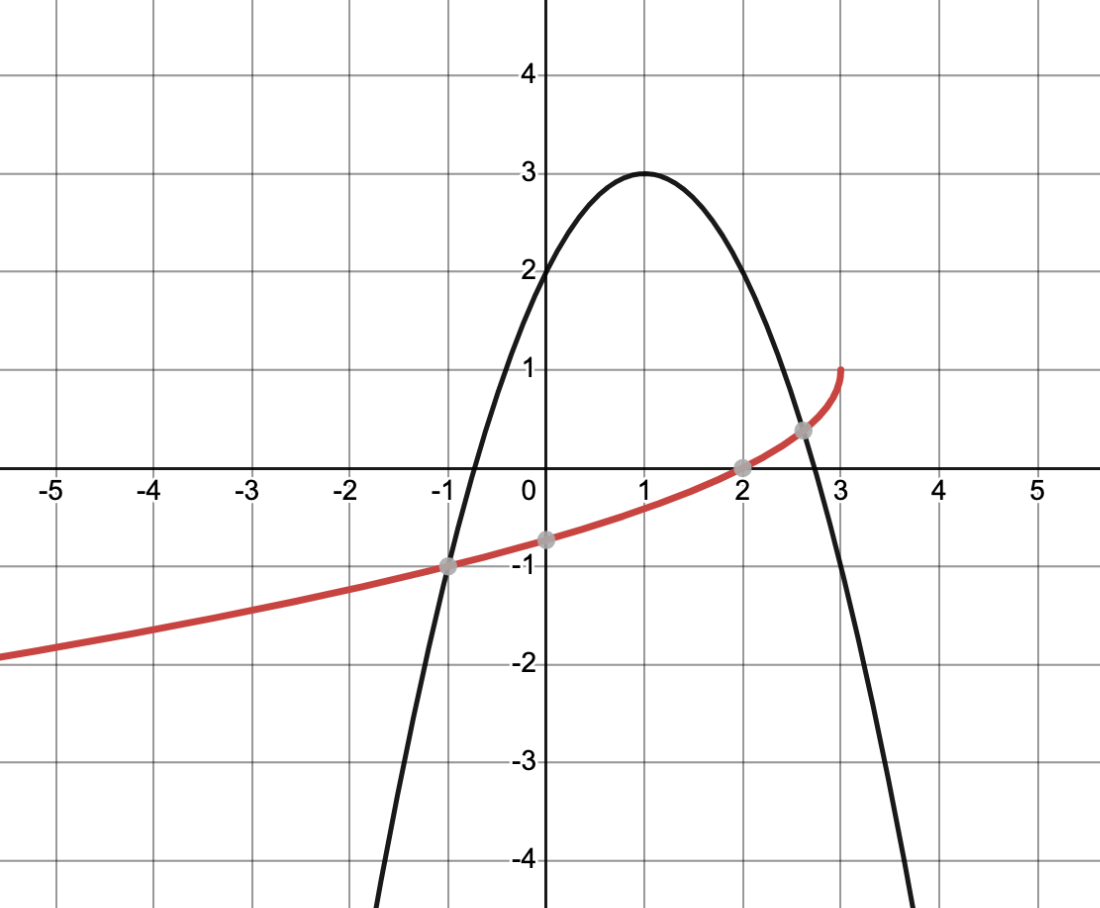
(-oo,1]
Find the average rate of change.
f(x) = 4x^2+7
[-2,3]
4(-2)^2+7
4(4)+7
16+7=23
4(3)^2+7
4(9)+7
36+7=43
(43-23)/(3--2)=20/5=4
Find the inverse equation.
f(x)=(x^2+4)^3
x=(y^2+4)^3
root(3)(x)=y^2+4
root(3)(x-4)=y^2
f^-1(x)=sqrt(root(3)(x)-4)
Find the equation and domain of the INVERSE.
f(x) = 2x^2 -4
y=2x^2-4
x=2y^2-4
x+4=2y^2
(x+4)/2=y^2
f^-1(x)=sqrt((x+4)/2)
[-4,oo)
Find the point of symmetry of the INVERSE function.
f(x)=-(x+2)^3-6
x=-(y+2)^3-6
x+6=-(y+2)^3
-x-6=(y+2)^3
root(3)(-x-6)=y+2
root(3)(-x-6)-2=y
(-6,-2)
Name 3 possible restrictions to ensure the inverse would be a function.
f(x)=2x^2-5
[0,oo)
(-oo,0]
[1,oo)
Find the average rate of change
f(x)=2(x-4)^3+1
[1,4]
f(1) = 2(1-4)^3+1
f(1)= 2(-27)+1
f(1)=-53
f(4)=2(4-4)^3+1
f(4)=1
(1--53)/(4-1)
54/3=18
Find the inverse equation.
f(x)=sqrt(5x^3)+1
x=sqrt(5y^3)+1
x-1=sqrt(5y^3)
(x-1)^2=5y^3
((x-1)^2)/5=y^3
f^-1(x)=root(3)(((x-1)^2)/5)