Benenne die Termstruktur:
a2
a+b
a(b+c)
a2 -> Potenz/ Quadrat
a+b -> Summe
a(b+c) -> Produkt
Bei welcher Funktionsgleichung handelt es sich nicht um eine lineare Funktion?
a) f(x) = x2-5
b) f(x) = 2
c) f(x) = 5x-1
a)
Nenne den Satz des Pythagoras (Voraussetzung und Behauptung!)
Wenn in einem Dreieck ABC an der Ecke C ein rechter Winkel ist, dann gilt a2+b2=c2.
Benenne die Körper.
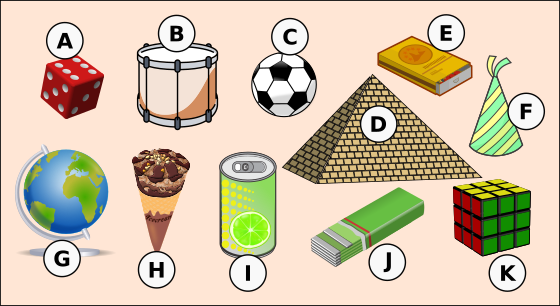
A - Würfel (Quader)
B - Zylinder
C - Kugel
D - Pyramide
E - Quader (Prisma)
F - Kegel
G - Kugel
H - Kegel
I - Zylinder
J - Quader (Prisma)
K - Würfel
Bestimme den Definitionsbereich: 2a/(a+3)
a aus den reellen Zahlen, a≠-3
Wofür steht k in der allgemeinen Gleichung für lineare Funktionen: y=kx+d ?
die Steigung der Funktion
Berechne die fehlende Seitenlänge eines rechtwinklige Dreiecks ABC mit dem rechten Winkel bei gamma und a =13cm und c = 25cm
b = 21,35cm
Eine Pyramide hat eine rechteckige Grundfläche mit a=5cm und b=10cm und eine Höhe von 22cm.
Wieviele dieser Pyramiden passen in einen Quader mit den Maßen a=5cm, b=10cm und c=22cm?
3
Nenne die 1. binomische Formel: (a+b)2...
...=a2+2ab+b2
An welcher Stelle schneidet die Funktion y=2x-5 die x-Achse?
Bei 5/2=2,5
Nenne zwei Eigenschaften von Original- und Bildfigur, die beim Vergrößern im Verhältnis 1 : 5 erhalten bleiben.
Winkelgrößen
Streckenverhältnisse
Flächenverhältnisse
Lage von Geraden zueinander (Parallelität, rechter Winkel)
Wenn man bei einem Zylinder den Radius verdoppelt, um welchen Faktor vervielfacht sich dann das Volumen.
Es vervierfacht sich (4).
Gegeben ist ein Quadrat mit a als Seitenlänge. Das Quadrat wird an beiden Seiten um 2cm verlängert. Gib einen Term für den Flächeninhalt der neuen Fläche an.
(a+2)2
An welcher Stelle schneiden sich die Funktionen f und g?
f(x) = 3x-1
g(x) = 0,2x-1
Bei (0;-1)
Benenne alle ähnlichen Figuren.
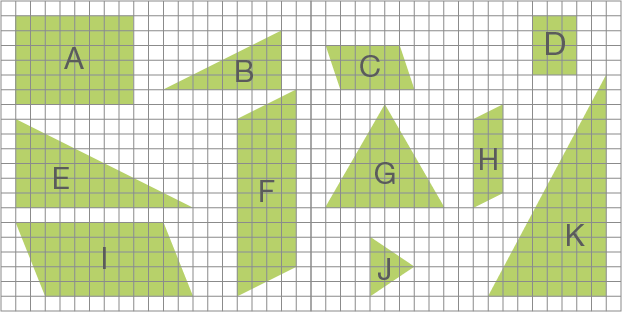
A und D
B und E (nicht K)
F und H
NICHT G und J, C und F, I
Gib eine Formel an, um das Volumen des dreiseitigen Prismas zu berechnen (die Basis ist ein rechtwinkliges Dreieck):
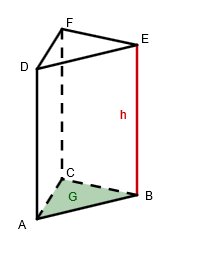
V = 0,5(a*b)*h
Forme in ein Produkt um: x2-16
x2-16=(x+4)(x-4)
Ein Swimmingpool mit einem Fassungsvermögen von 1200l wird mit einem Gartenschlauch befüllt, aus dem 9 Liter Wasser pro Minute fließen. Stelle eine Funktionsgleichung auf, die den Zusammenhang zwischen der vergangenen Zeit und dem Füllvolumen des Swimmingpools darstellt.
y = 9x
Ein Quader hat die Seitenlängen AB=15cm, BC=4cm und AE=10cm.
Berechne die Länge der Diagonale AF.
AF=18,47cm
Gib einen Term zur Berechnung des Volumens des abgebildeten Körpers an:
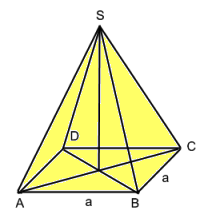
V = (a² * h) / 3