Easy
Medium
Hard
Conceptual Qs
Double Jeopardy
100
If y=cos2x, then dy/dx=
(A) -2sin2x (B) -sin2x
(C) sin2x (D) 2sin2x (E) 2sinx
(A) -2sin2x
100
lim x->∞
sqrt(9x^4+1)/(4x^2+3)
is
(A) 1/3 (B) 3/4 (C) 3/2 (D) 3/2 (E) DNE
(B) 3/4
100
If y=(x/(x+1))^5 then dy/dx=
(A) 5(1+x)^4
(B) (5x^4)/(x+1)^4
(C) (5x^4)/(x+1)^6
(D)(5x^4(2x+1))/(x+1)^6
(C) 5x^4/(x+1)^6
100
If y=f(x) is a solution to the differential equation below with initial condition f(0)=2, which of the following is 2?
dy/dx=e^(x^2)
(A) 1+e^(x^2)
(B) 2xe^(x^2)
(C) int_0^x e^(t^2)dt
(D) 2+int_0^x e^(t^2)dt
(E) 2+int_2^x e^(t^2)dt
(D) 2+int_0^x e^(t^2)dt
100
A slope field for a differential equation is shown in the figure above. If y=f(x) is the particular solution to the differential equation through the point (-1,2) and h(x)=3x∗f(x), then h'(-1)=
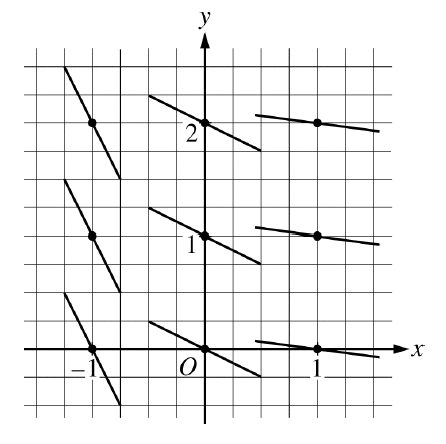
12
200
The slope of the line tangent to the graph of y=ln(1-x) at x=-1 is
(A) -1 (B) -1/2 (C) 1/2 (D) ln2 (E) 1
(B) -1/2
200
If 0<c<1, what is the area of the region enclosed by the graphs of y=0, y=1/x, x=c, and x=1?
(A) ln(1-c) (B) ln(1/c) (C) ln(c)
(D) 1/c2 - 1 (E) 1 - 1/c2
(B) ln(1/c)
200
int_0^4x/sqrt(x^2+9)dx=
(A)-2
(B) -2/15
(C) 1
(D) 2
(D) 2
200
The table above gives selected values for a twice-differentiable function f. Which of the following must be true?
(A) f has no critical points in the interval -1<x<5
(B) f'(x)=8 for some value in the interval -1<x<5
(C) f'(x)>0 for all values in the interval -1<x<5
(D) f''(x)<0 for all values in the interval -1<x<5
(B) f'(x)=8 for some value in the interval -1<x<5 (MVT)
300
int(e^x+e)dx=
(A) e^x+C
(B) 2e^x+C
(C) e^x+e+C
(D) e^(x+1)+ex+C
(E) e^x+ex+C
(E) e^x+ex+C
300
Let h be the function defined by the integral below. Which of the following is an equation for the line tangent to the graph of h at the point where x=π/4 ?
h(x)=int_(pi/4)^x(sin^2t)dt
(A) y=1/2
(B) sqrt(2)
(C) y=x-pi/4
(D) y=1/2(x-pi/4)
(E) y=sqrt(2)/2(x-pi/4)
(D) y=1/2(x-pi/4)
300
Sand is deposited into a pile with a circular base. The volume V of the pile is given by V=r3/3 , where r is the radius of the base in feet. The circumference of the base is increasing at a constant rate of 5pi feet per hour. When the circumference of the base is 8pi feet, what is the rate of change of the volume of the pile?
(A) 8/pi (B) 16 (C) 40 (D) 40pi (E) 80pi
(C) 40
300
Let f be a function that is continuous on the closed interval [1,3] with f(1)=10 and f(3)=18. Which of the following statements must be true?
(A) 10<f(2)<18
(B) f is increasing on the interval [1,3]
(C) f(x)=17 has at least one solution in the interval [1,3]
(D) f'(x)=8 has at least one solution in the interval (1,3)
(C) f(x)=17 has at least one solution in the interval [1,3] (IVT)