End Behavior
Zeroes
Vertical Asymptotes and Holes
Equivalent Representations
Transformationmations
Mathematics to Tease the Brain
100
The lim_(x->oo) f(x) , given the following function.
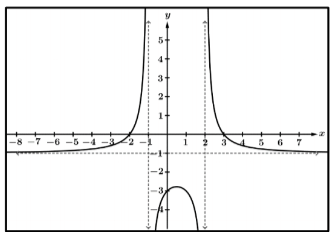
What is -1?
100
The intervals of this function where f(x)<=0 .
What is (-3,-1] and [2,3)?
100
The holes and vertical asymptotes in
k(x)=((x-1)(x+3))/((x+3)(x-2)
What is a vertical asymptote at x=2 and a hole at x=-3?
100
Determine if the following function has a horizontal asymptote, slant asymptote, or neither:
f(x)=(3x^3-4x+6)/(x^2-3)
What is a slant asymptote?
100
Given that h(x)=-2g(x-3)-5 , the value of h(0).
What is 3?
100
Effective storage of the worlds busiest workers. Name this shaped storage used by bees to store honey in the most efficent way using the minimal amount of wax.
What is the honeycomb structure?
200
The horizontal asymptote present when the degree of the numerator is smaller than the degree of the denominator.
What is
y=0?
200
The intervals of this function where f(x)>=1 .
What is (-oo, -3) and (3, oo)?
200
The holes and vertical asymptotes in the following function:
y=((x-2)^2(x+3)(x-5)^6)/((x-2)^3(x+3)(x-5)^2)
What is a hole at x=-3 and x=5 and a vertical asymptote at x=2?
200
Determine if the following function has a horizontal asymptote, slant asymptote, or neither:
h(x)=(x(x-3)^2)/(3x^3-2)
What is a horizontal asymptote?
200
Given that g(x)=3f(x+2)-1 , the value of g(-2).
What is -2?
200
While Pascal's triangle is wonderful, it is actually an extension of a previous pattern. Follow a single diagonal of the triangle and you will arrive at this pattern, one where each number is the sum of the previous two.
What is the Fibonacci sequence?
300
The horizontal asymoptote given by the rational function r(x)=f(x)/g(x) where f(x)=2x^3+4x-1 and g(x)=6x^3-x^2+4 .
What is
1/3
300
Solve the following inequality: ((x-1)(x+2)^2)/(x-2)>=0 .
What is (-oo,1] and (2,oo)?
300
An expression for h(x) given that the graph has a hole at x=-4, a vertical asymptote at x=-5, and a zero at x=1/2.
What is
h(x)=((x+4)(x-1/2))/((x+4)(x-5))=((x+4)(2x-1))/((x+4)(x-5))
300
Determine if the following function has a horizontal asymptote, slant asymptote, or neither:
y=((x+3)^2(2x^2-4)^2)/(x^2(x-5)(x+6)^3
What is a horizontal asymptote?
300
Given that h(x)=5-f(2x) , the value of h(2)
What is 3?
300
Nat"A mathematician confided, this strip here is one-sided. You'll get quite a laugh if you cut one in half, for it will stay in one piece when divided."
Name this mathematic shape that only has one side, which only has one side, and shares a name with a beloved Matrix character.
What is the Mobius strip?
400
The graph of a function that:
increases in height as the inputs decrease without bound,
decreases in height as the inputs increase without bound.
What is a graph with the following:
lim_(x->-oo)f(x)=oo; lim_(x->oo) f(x)=-oo
400
Solve the following inequality:
(4x-8)/(x+5)<=0.
What is (-5,-2]?
400
An expression for g(x) given the graph below:
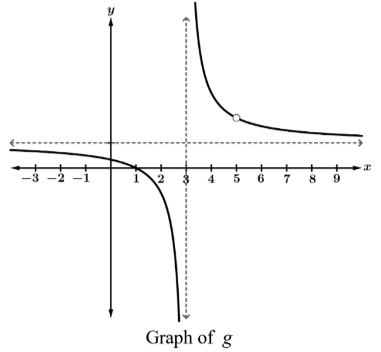
What is
((x-1)(x-5))/((x-5)(x-3)
400
The remainder from the following long division:
(x^3+2x^2-3x+4) divide (x-7)
What is 424?
400
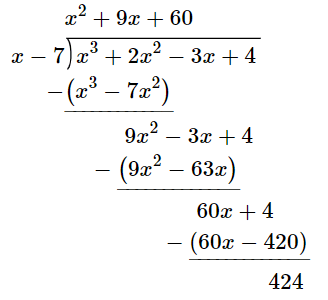
The equation of h(x) given that it is the result of applying the following three transformations to j(x): a horizontal dilation by a factor of 1/3, a vertical dilation by a factor of 2, and a vertical translation by -4 units.
What is
h(x)=2j(3x)-4?
400
A series of seashells spiraling in to infinity, a pattern that exists in everything from the human face, to the spines of a pinecone, to the seeds of a sunflower. Name this splended pattern, the ratio of all things that when shows a proportianl structure with a value of 1.618.
What is the golden ratio?
500
The limits of y as it increases and decreases without bound, given y=(4x+3)^2/((3x-1)(2x+5) .
What is y=8/3?
500
Solve the following inequality: (x^2-4)/(x^2-10x+25)<0 .
What is (-2,2)?
500
The holes and vertical asymptotes of the function r(x) given that r(x)=f(x)/g(x) , f(x)= x^3-100x , and g(x)=x^2-5x-50 .
What is a hole at x=10 and a vertical asymptote at x=-5?
500
The remainder from the following long division:
(3x^4-5x^2+3) divide (x+2)
What is 31?
500
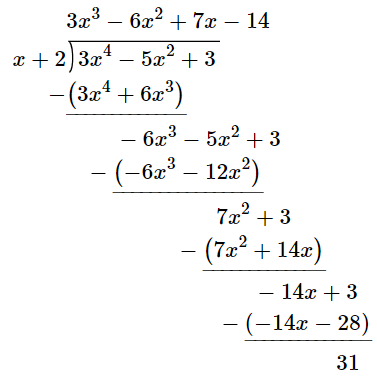
The domain and range of k(x) given that k(x)=-3f(2x)+1 and the function f(x) has the domain [-3,3] and the range [-5,3].
What is the domain [-3/2, 3/2] and range [-8,16]?
500
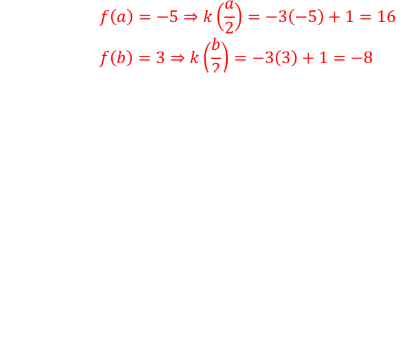
As plants grow they branch out into new buds that repeat the same shape of the original plant. These buds eventually do the same creating a pattern of repeated objects each smaller than the last. Name this pattern found in all things from tree branches, ferns, coastlines, and is even mentioned in a disney film regarding snowflakes?
What is a fractal pattern?