sin(pi/3)=
sqrt3/2
csc(pi/6)=
2
sin^2x+cos^2x=
1
cosx=sqrt2/2; x=
pi/4, (7pi)/4
What function is this
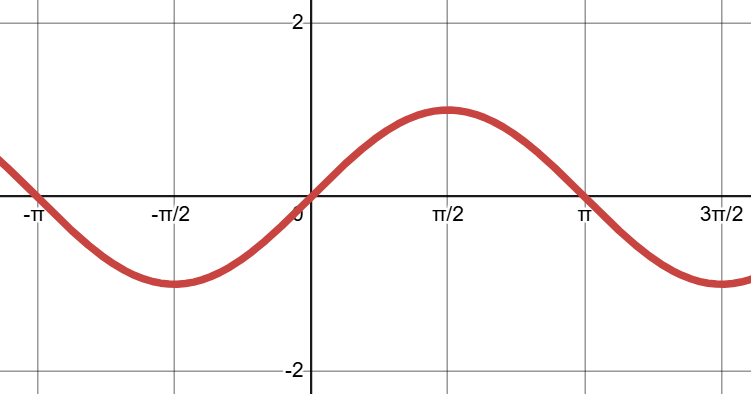
Sinx
cos^-1(-1)=
pi
sec((5pi)/6)=
-2/sqrt3
cscx*cosx=
cotx
2sinx+1=-1; x=
(3pi)/2
What's the function?
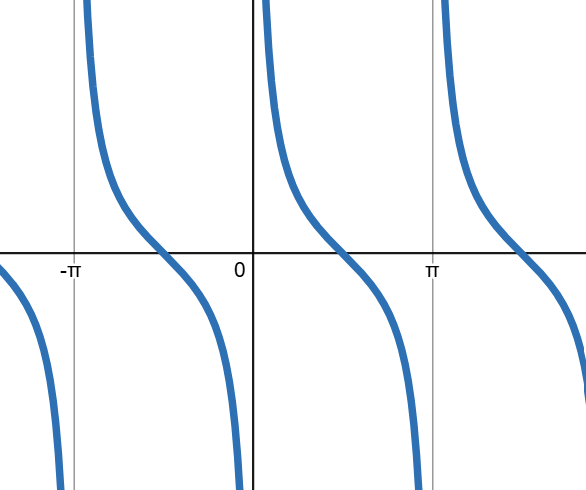
cotx
tan((2pi)/3)=
-sqrt3
cot((7pi)/6)=
sqrt3
1+cot^2x=
csc^2x
Find all solutions on the interval [0, 2π]
cos2x=1/2
pi/6, 5pi/6, 7pi/6, 11pi/6
Identify the first two vertical asymptotes
cot(x/2); 0<=x
x=0, 2pi
sin((-17pi)/6)=
-1/2
sec((19pi)/3)=
2
sin((3pi)/4+pi/6)=
(sqrt6-sqrt2)/4
2sin^2x-sinx-1=0; x=
x=pi/2, 7pi/6, 11pi/6
Determine the amplitude and period of the function
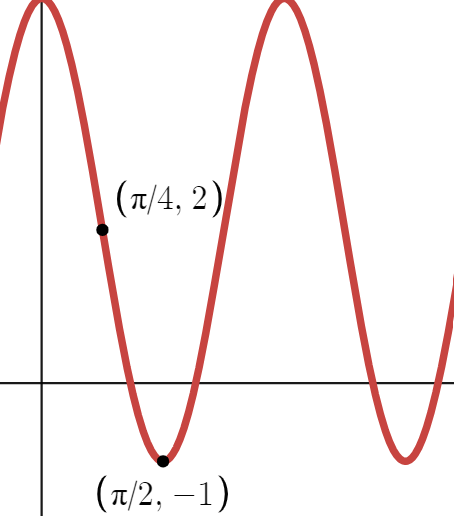
Amplitude = 3
Period=π
Write an equation to model the position of point P:
The height of the center of a windmill is 14 feet above the ground. Point P is at the end of an arm, which is 6 feet long. Point P starts directly above the center and completes one rotation every 4 seconds.
6cos((pit)/2)+14
6sin(pi/2(t+1))+14
Give the coordinates of the first local minimum and first local maximum of
4csc(2x); 0<x
min=(pi/4, 4)
max=((3pi)/4, -4)
2cos^2x-1=
cos2x
1-2sin^2x
cos^2x-sin^2x
1+cosx=sin^2x; x=
x=pi/2, pi, 3pi/2
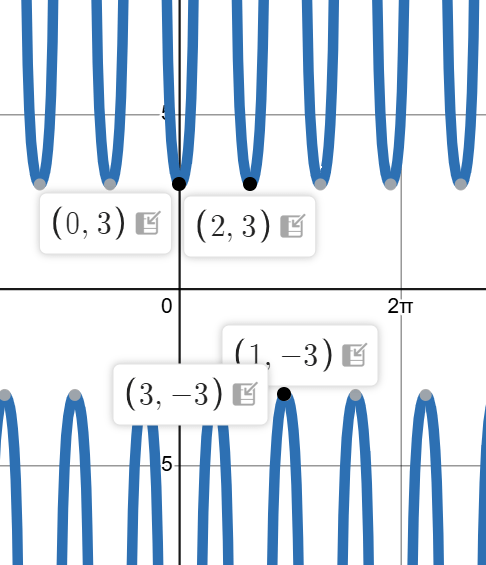
Graph (and label 4 points) for the following function
3sec(pix)