Function Characteristics
Inverse & Compositions
Rational Functions
Exponential Functions
Logarithms
100
Find the average rate of change over the interval [-3, 1].
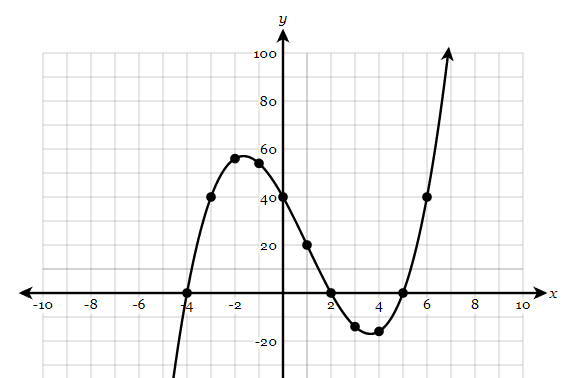
(-3, 40) and (1, 20)
(y_2-y_1)/(x_2-x_1)=(20-40)/(1-(-3))=-20/4
AROC=-5
100
Determine f^-1(f(5)) for the function below.
f(x)=1/2x-3
By definition f^-1(f(5))=5
100
Determine the value of x in the equation below.
(x-3)/(4x)=2/3
(3)(x-3)=(2)(4x)
3x-9=8x
-9=5x
x=-9/5
100
Rewrite the power below in rational form.
z^(2/7)
root(7)(z^2)
100
What is the value of y in the equation below?
log_y 64=3
y = 4
200
State the domain of the graph below.
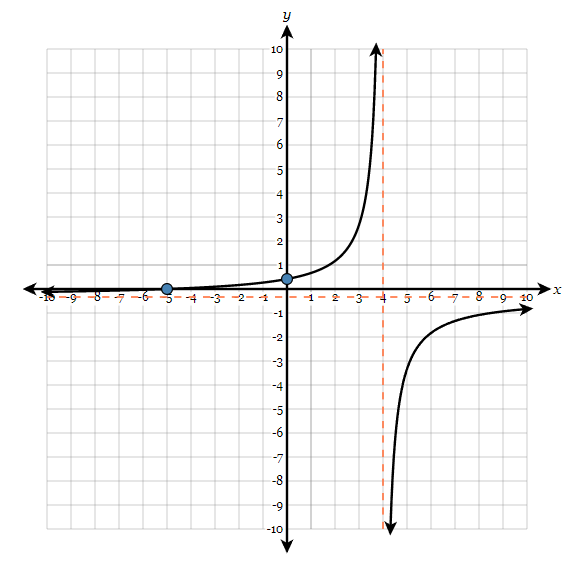
(-\infty,4)\cup(4,\infty)
200
Find the inverse of the function below.
g(x)=5x^2-4
y=5x^2-4
x=5y^2-4
x+4=5y^2
(x+4)/5=y^2
y=sqrt((x+4)/5)
200
Simplify:
(x^2-9)/(x^2-3x)\div(x^2+x-6)/(5x)
KCF:
(x^2-9)/(x^2-3x)\times(5x)/(x^2+x-6)
((x+3)(x-3))/(x(x-3))\times(5x)/((x+3)(x-2))
5/(x-2)
200
Determine the equation for the function in the table below.
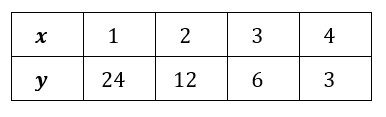
y=a(b)^x
b=12/24=1/2 or 0.5
a=48
y=48(1/2)^x
200
Expand the logarithm:
log(5^2x^7)
2log(5)+7log(x)
300
Determine the roots of the equation below.
y=x^3-13x-12
x = 4
x = -1
x = -3
300
What is the value of h(f(6)) ?
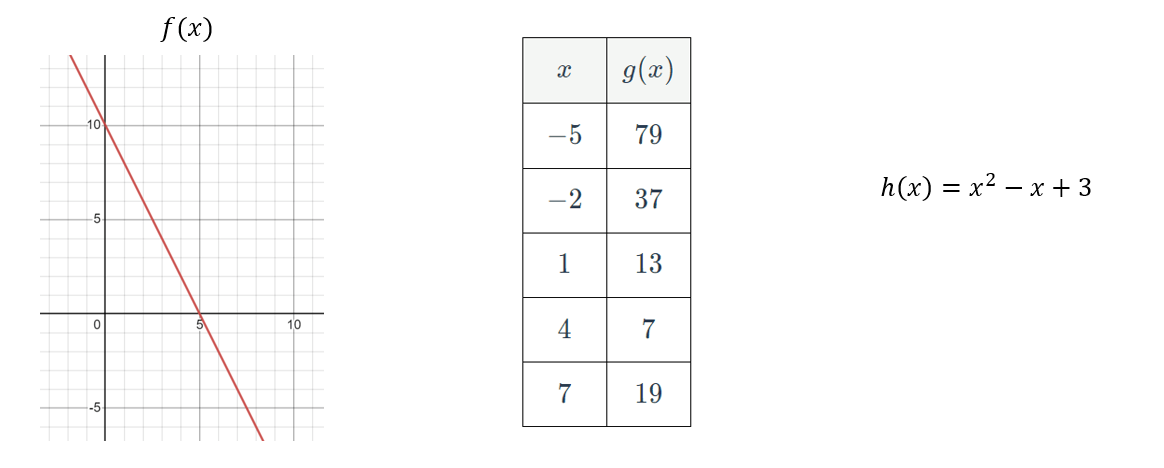
f(6)=-2
h(-2)=(-2)^2-(-2)+3
h(-2)=4+4+3
h(-2)=11
300
Determine the coordinates of the removeable discontinuity.
f(x)=(x^2-9)/(x^2-x-12)
f(x)=((x-3)(x+3))/((x-4)(x+3))
f(x)=(x-3)/(x-4)
RM: x=-3
f(-3)=(-3-3)/(-3-4)=(-6)/-7=6/7
(-3, 6/7)
300
Element X is a radioactive isotope such that every 13 years, its mass decreases by half. Given that the initial mass of a sample of Element X is 8800 grams, how much of the element would remain after 25 years, to the nearest tenth of a gram?
A(25)=8800(1/2)^(25/13)
A(25)=2320.5
300
Determine the solution(s) to the equation below.
log(x^2-x)=log(20)
x^2-x=20
x^2-x-20=0
(x-5)(x+4)=0
x=5, x=-4
400
Determine the domain of the function below.
f(x)=(x^2-4)/(x^2-3x-10)
f(x)=((x+2)(x-2))/((x-5)(x+2))
(-\infty,-2)\cup(-2,5)\cup(5,\infty)
400
What is the value of h(f(g^(-1)(7))) ?
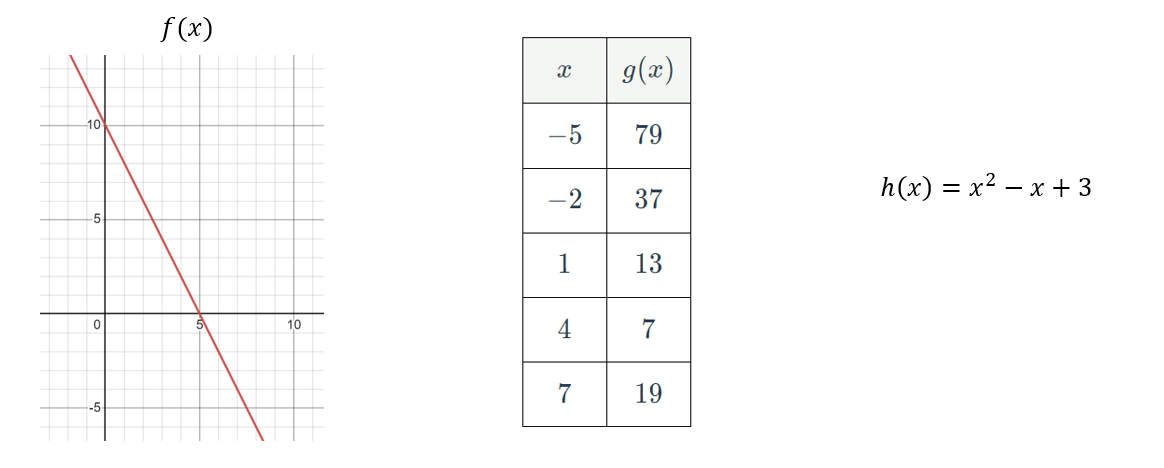
g^(-1)(7)=4
f(4)=2
h(2)=(2^2)-(2)+3=4-2+3
h(2)=5
400
Solve for m:
m/(m-2)+6/(m+4)=(4m+4)/(m^2+2m-8)
m/(m-2)+6/(m+4)=(4m+4)/((m+4)(m-2))
(m(m+4))/((m-2)(m+4))+(6(m-2))/((m=4)(m-2))=(4m+4)/((m+4)(m-2))
m(m+4)+6(m-2)=4m+4
m^2+4m+6m-12=4m+4
m^2+6m-16=0
(m+8)(m-2)
m=-8, m=2
m=-8
400
Solve for x:
(1/27)^(2x-1)=(81)^(x+5)
(3^-3)^(2x-1)=(3^4)^(x+5)
3^(-6x+3)=3^(4x+20)
-6x+3=4x+20
3=10x+20
-17=10x
x=-17/10
400
Juele invested $7,300 in an account paying an interest rate of 1.5% compounded quarterly. Assuming no deposits or withdrawals are made, how long would it take, to the nearest tenth of a year, for the value of the account to reach $8,560?
8560=7300(1+.015/4)^(4t)
1.17=(1+.015/4)^(4t)
log_(1+.015/4)(1.17)=4t
42.5=4t
t=10.6