Functions
Miscellaneous
Logarithms
Trig
Polynomials
100
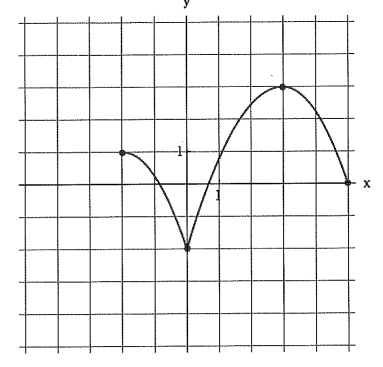
Find the domain & range.
Domain: [-2,5]
Range: [-2,3]
100
If $15,000 is invested at an interest rate of 4.75% per year, compounded continuously, find the value oft he investment after 10 years.
$24,120.21
100
ln(e^(2x - 5))
2x - 5
100
Find the terminal point for
t = (2pi)/3
(-1/2, sqrt(3)/2)
100
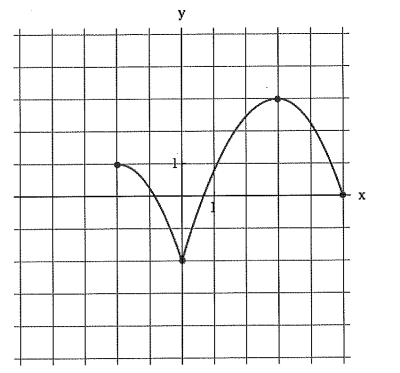Find the domain and range in interval notation.
Domain: [-2,5]
Range: [-2,3]
200
If f(x) = 3/x and g(x) = 2x + 3, find f(g(x))
1/(2x + 3)
200
Solve the inequality:
(x + 2)/((x - 1)(x - 5))>=0
[-2,1) U (5,oo)
200
Solve for x:
log4(3x + 1) = 3
x = 21
200
Find the exact value:
tan((11pi)/6)
-sqrt(3)/3
200
Find the average rate of change from t = 2 to t = 5 for
f(t) = t^3 + 3t
10
300
Find the domain of
f(x) = 5/(x + 3)
x != -3
(-oo,-3) U(-3, oo)
300
A soft-drink vendor at a popular beach analyzes his sales records and finds that if he sells x cans of soda pop in one day, his profit (in dollars) is given by P(x). What is his maximum profit per day, and how many cans must he sell for maximum profit?
P(x) = -0.001x^2 + 4x - 1875
Max Profit: $2125
How many cans? 2000
300
Use the Laws of Logarithms to expand the expression.
log((x^5 sqrt(y))/z^3)
5 log x + (1/2)log y - 3 log z
300
Find the cos t if sint = 7/25 and the terminal point t is in the II quadrant
-24/25
300
Two polynomials P and D are given. Use either synthetic or long division to divide P(x) by D(x).
P(x) = 2x^3 + x^2 + 3x + 7, D(x) = x + 2
2x^2 - 3x + 9 -11/(x+2
400
Find the inverse of
f(x) = 2x^3 +4
root(3)((x - 4)/2
400
Find an equation of the line that passes through (1,-5) and is perpendicular to the line 3y -2x = 3
y = (-3/2)x - (7/2)
400
Use the Laws of Logarithms to combine the expression.
5 log(x) +3 log y - log(z − 1)
log((x^5y^3)/(z - 1))
400
Find the amplitude, period, and phase shift of the function
y = -4sin3(x + pi/2)
A = 4
P =
(2pi)/3
Phase shift: Left
pi/2
400
Find the horizontal and vertical asymptotes for:
(3x^2 + 4)/(x^2 - 4)
HA: y = 3
VA: x = 2, x = -2
500
Express in vertex form:
f(x) = x^2 + 4x + 9
f(x) = (x + 2)^2 +5
500
Solve the equation graphically in the interval [-1,5]. State answer(s) rounded to two decimals
x^3 + 14.2x^2 -4.8x - 12.4 = 0
-0.80, 1.08
500
For the following equation, find the exact solution of the exponential equation in terms of logarithms.
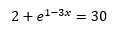
2 + e^(1-3x) = 30
(ln(28) - 1)/-3
500
Evaluate:
cos^-1 (-1/2)
(2pi)/3
500
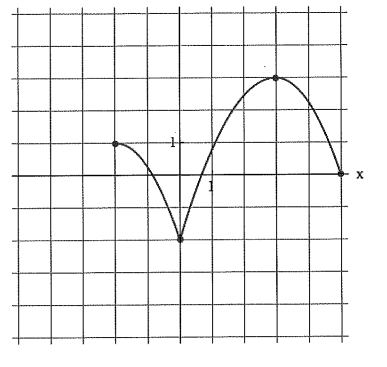
Find the interval(s) where f is increasing; where f is decreasing.
Increasing: (0,3)
Decreasing (-2,0) and (3,5)