What is the slope ("m") and y-intercept ("b") of the following equation?
y=3x-2
the slope is 3 and the y-intercept is -2
When solving a system of equations using substitution, what's the first thing you need to look for?
the y
Find the value of x.
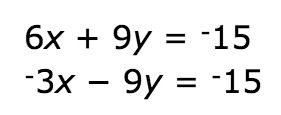
x=-10
What does Reduce mean?
simplify
What do we call more than one equation to be solved at the same time?
System of Equations
When graphically solving a system of equations, what represents your final answer?
The point of intersection, an ordered pair
Find the value of x.
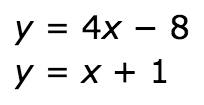
x=3
Find the value of y.
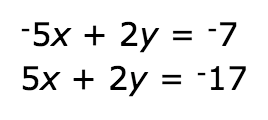
y=-6
True or false: I can use any method (graphing, substitution, or elimination) to solve any system of equations.
True
How many solutions does a graph with parallel lines have?
No Solutions
What is the solution to this system of equations? State your answer as an ordered pair.
(3,-2)
Find the value of x.
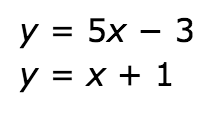
x=1
Find the value of y.
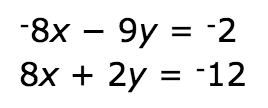
y=2
The goal of solving a system of equations is to...
find the values of ALL variables.
How many solutions does a graph with coincident (same) lines have?
Infinite (Many) Solutions
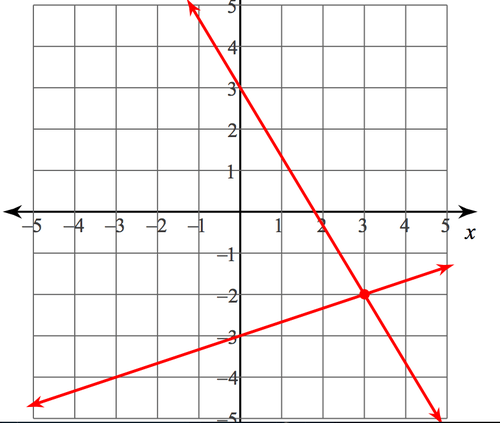
Graphically solve this system of equations. State your final answer as an ordered pair.
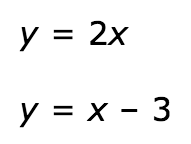
(-3,-6)
Solve the system of equations using substitution. State your final answer as an ordered pair.
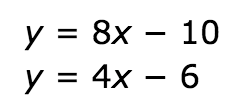
(1,-2)
Solve the system of equations using elimination. State your final answer as an ordered pair.
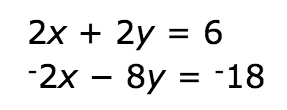
(1,2)
What should happen if a point is a solution to a system? Graphically
Graphically : where the lines intersect
Solve the system of equations :
y - 3x = 3
y = 3x - 2
No Solution
Graphically solve this system of equations. State your final answer as an ordered pair.
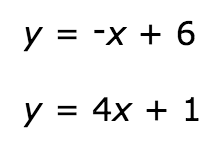
(1,5)
Solve the system of equations using substitution. State your final answer as an ordered pair.
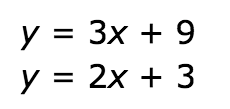
(-6,-9)
Solve the system of equations using elimination. State your final answer as an ordered pair.
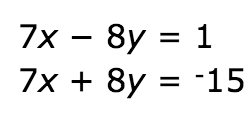
(-1,-1)
If you graphically solved a system of equations and found there was no solution, what could you conclude about the two lines?
The lines are parallel.
Solve the system :
x - 2y = 6
-4x + 8y = -24
Infinite (Many) Solutions