Transformations
Congruent Figures
Reflections
Rotations
Properties of Rigid Transformaitons
100
What tyoe of transformation involves moving a figure along a straight path without changing its position.
Translation
100
True or False: Two figures are congruent if one can be mapped onto the other using only translations, rotations, and refelections.
True
100
What happens to a figure when it is reflected over a line?
It is flipped across the line, creating a mirror image.
100
How many degrees are in full rotation?
360 degrees
100
Which of the following transformations preserves both the size and shape of a figure?
- A: Translation
- B: Rotation
- C: Reflection
- D: All of the above
D: All of the above
200
Explain why figure B is not the image of figure A after a 90* rotation around center P
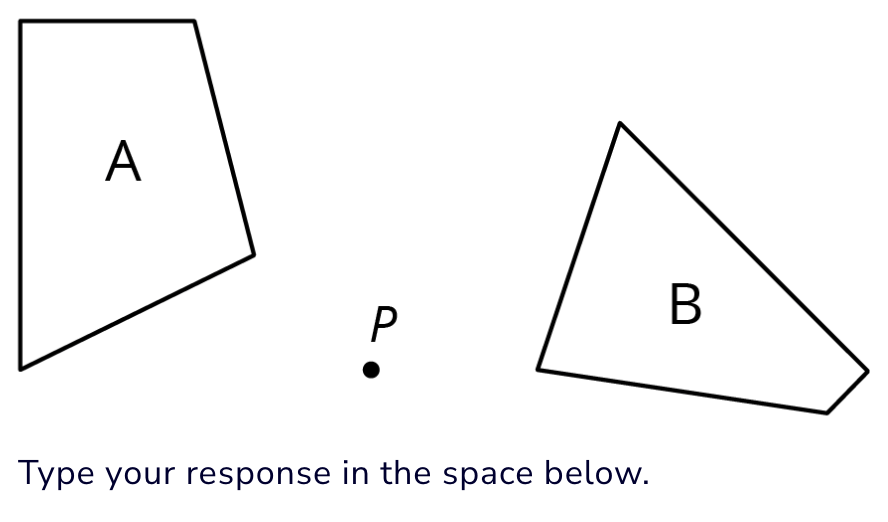
a. The shortest side of Figure A is shorter than the shortest side of Figure B. Since rotations do not change lengths, Figure B is not a rotation of Figure A.
b. The angles in Figure B do not match the corresponding angles in Figure A. Some of the angles in Figure A look like right angles while some corresponding angles in Figure B are definitely not right angles.
200
Can two rectangles be congruent if one has been rotated 90 degrees?
Yes, as long as the sides are equal in length.
200
What is the result of reflecting a shape twice over the same line?
The shape returns to its original position.
200
If a figure is rotated 90° clockwise, what transformation could undo the rotation?
A 90* counterclockwise rotation
200
Which property of a figure remains unchanged after a rigid transformaton?
- A: Area
- B: Shape
- C: Orientation
- D: Both A and B
D: Both A and B
300
Which sequence of transformations would NOT return a shape to its original position?
A: Translate 3 units up, then 3 units down.
B: Reflect over a line, then reflect over the same line again.
C: Translate 1 unit to the right, then 4 units to the left, then 3 units to the right.
D: Rotate 90° counterclockwise, then rotate 90° counterclockwise again.
D: Rotate 90° counterclockwise, then rotate 90° counterclockwise again.
300
Which of the following would prove that two quadrilaterals are congruent?
A: They have the same area.
B: They have the same side lengths and angles.
C: They have the same perimeter.
B: They have the same side lengths and angles.
300
True or False: A reflection changes the size of a shape.
False
300
True or False: A 180° rotation around the origin produces the same result as reflecting over both axes.
True
300
What is the name of the transformation that flips a figure over a line to create a mirror image?
Reflection
400
If a shape is rotated 180* about the origin, how does the position of the shape change?
The shape is upside down, but the size and shape remain the same.
400
How can you use rigid transformations to prove that two triangels are congruent?
By applying a combination of translations, rotations, or reflections to map one triangle onto the other.
400
Name a sequence of transformations that can take image P to image Q.
Teacher approved...
some examples: a reflection, and then a different reflection
a single rotation of 180* using (0,0) as the center
400
If a figure is rotated 270° counterclockwise, what is the equivalent clockwise rotation?
90* clockwise
400
Which of the following transformations changes the orientation of a figure but keeps it congruent to the original?
- A: Rotation
- B: Reflection
- C: Translation
- D: None of the above
B: Reflection
500
Point A is located at (-4,3) If you rotated A 180 degrees using (0,0) as your center, what are the coordinates of its image A'?
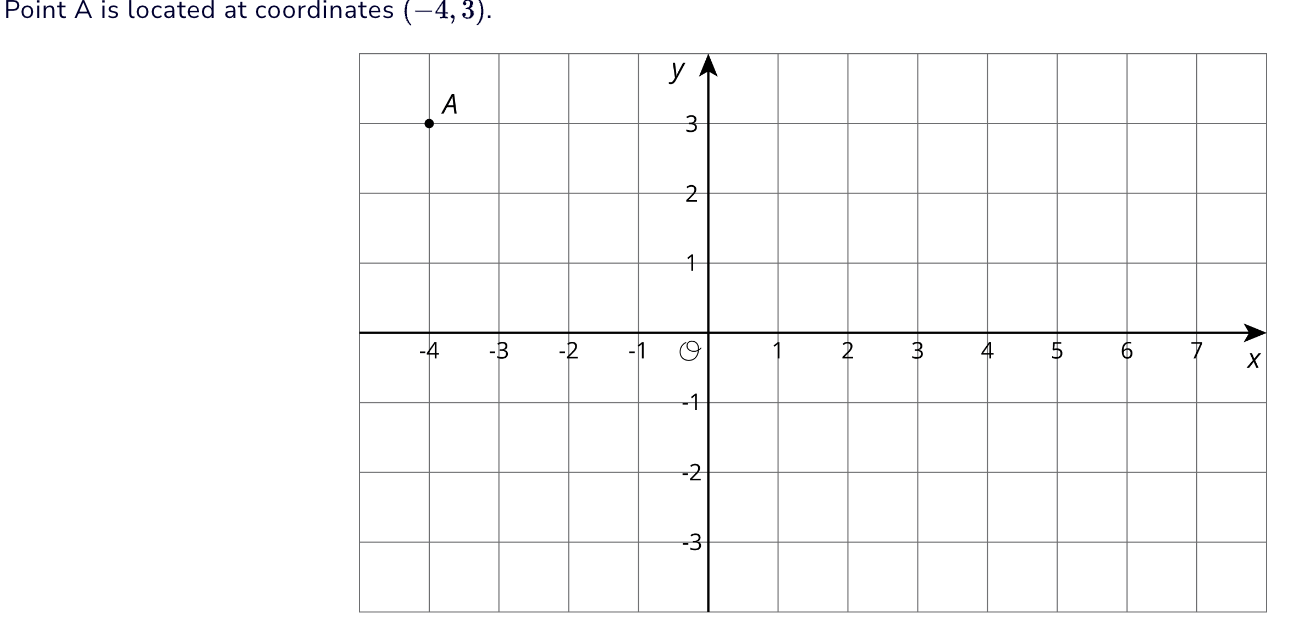
A' (4,-3)
500
Name all three requirements needed to perform a rotation.
Direction (clockwise, counterclockwise)
Angle (how far to rotate)
center of rotation (what are we rotating about?)
500
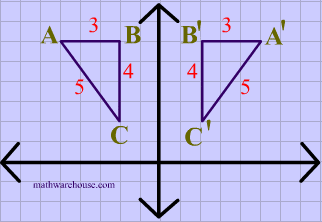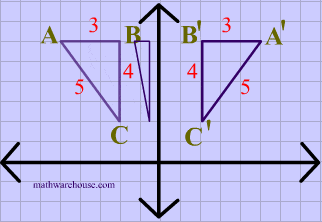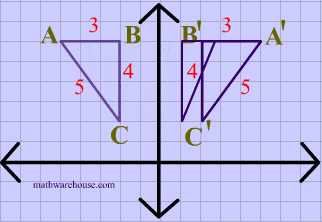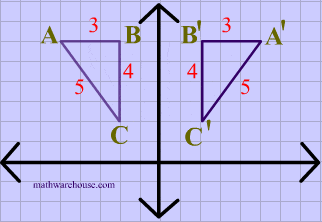What transformation is this?
It's a reflection over the Y axis
500
How many kids does Mr. B have!
Mr. B has 2 kids
age 2.5yrs
age 4.5 years
500
Which rigid-transformaiton ALWAYS changes the position of a figure but keeps it congruent to the original?
A: Rotation
B: Reflection
C: Translation
D:A and B
D: Both A and B (Rotation changes orientation in some cases, but reflection always does).