Definitions
Transformations
Symmetry
Proof by Transformation
Slopes & Lines
100
Freebie: Draw an emoji based on how you're feeling for the test
:)
100
What are the 3 transformations we have discussed in unit 1?
translation, rotation, reflection
100
What is a line of symmetry?
The vertical line that divides the graph or figure into two congruent halves, sometimes called axis of symmetry.
100
What is congruency?
Two geometric figures are defined to be congruent if there is a sequence of rigid motions that carries one onto the other.
Congruency of angles and side lengths have the same measure.
100
In the equation of a line y=mx+b,
which letter represents slope?
m
200
What is a translation?
A transformation that locates points at the same distance and direction along lines that are parallel to each other
200
Describe the transformation
reflection over y=x
200
If a figure has rotational symmetry, it means...
the figure can be carried onto itself by a rotation of a certain degree.
200
How can I prove with rotations that angle C is congruent to angle A?
rotate 180 degrees
200
Perpendicular lines intersect at a 90 degree angle because their slopes are _________ _____________, while parallel lines never intersect because their slopes are ____ ____________.
opposite reciprocals
the same
300
What is a rotation?
A transformation that locates points in the same direction along concentric circles and through the same angle of rotation around the center of rotation.
300
What is the transformation below?
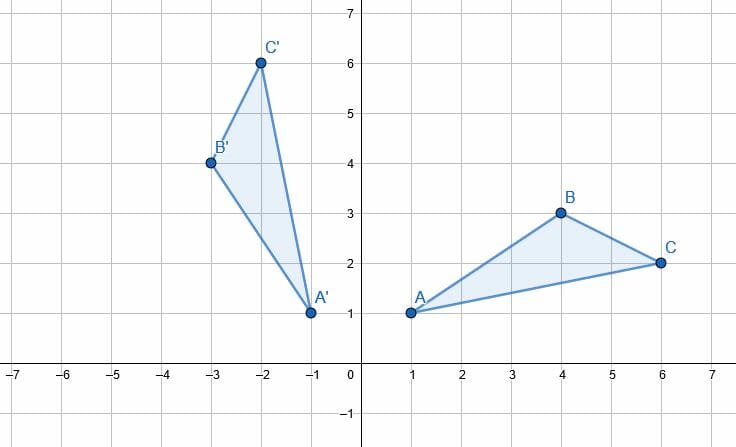
Rotation 90 degrees counterclockwise around the origin (0,0)
300
Draw all lines of symmetry for the regular polygon again, then list the angles satisfying its rotational symmetry.
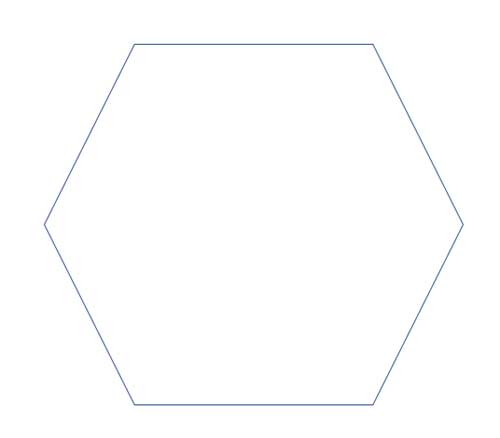
(lines of symmetry through each vertex, 5 lines)
72, 144, 216, 288, 360
300
Prove, with transformations, that BC is congruent to AE
Rotation and reflection
Reflection and translation
300
Create an equation that is parallel to y= 3/5x+7
y=3/5x + b
(b is any number)
400
What is a reflection?
A transformation that locates points across a line of reflection so that the line of reflection is a perpendicular bisector of each line segment connecting corresponding pre-image and image points.
400
Determine the transformation and write the rule.
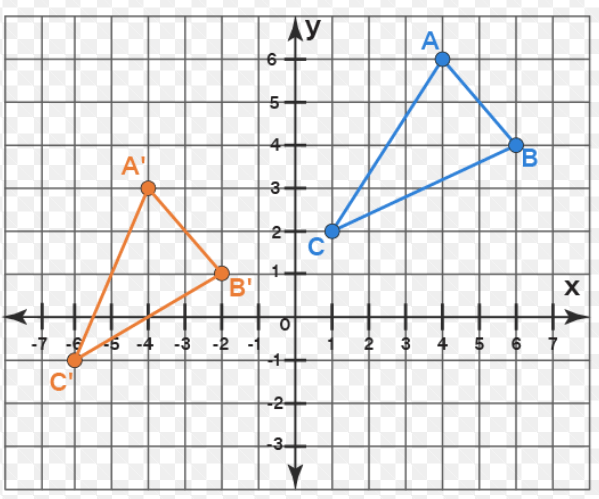
translation
f(x,y)= (x-8, y-3)
400
Draw the lines of symmetry for the equilateral triangle below. Then list the angles satisfying its rotational symmetry.
3 lines
60, 120, 180
400
How can you prove, with transformations, that the two figures are congruent?
translation doesn't change side length or angle measure, therefore the measure of angle A is the same as A', which applies to all angles and side lengths.
400
Create the equation of a line that is perpendicular to the line given below
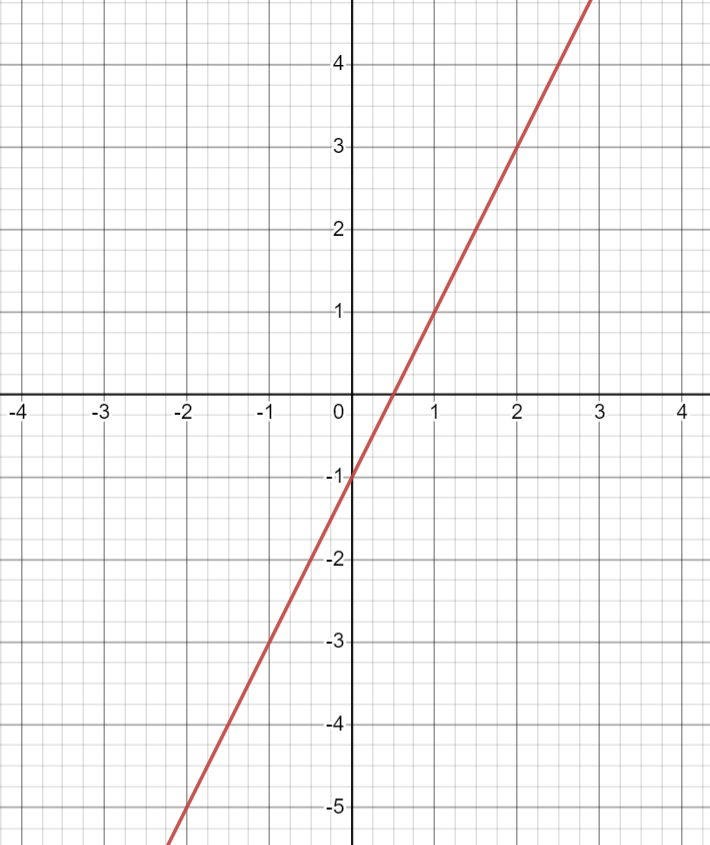
y= -1/2x (+ or - any b)
500
What is a rigid transformation?
Any transformation that will preserve distance and angle measure of a figure.
500
The coordinates for triangle ABC is A(-2,0) B(0,4) C(-4,3).
What would the coordinate points be for triangle A'B'C' when the function rule f(x,y)= (-y,x) is used?
A' (0,-2)
B' (-4,0)
C' (-3,-4)
500
If my rotational angles are multiples of 30 (i.e. 30, 60, 90, 120,...360)
How many sides of the regular polygon are there?
12
360/12=30
500
Prove, with transformations, how DA is congruent to AB
Reflection over CA
500
Find the equation of the given line, create an equation of a line parallel to the given line, AND create an equation that is perpendicular to the given line.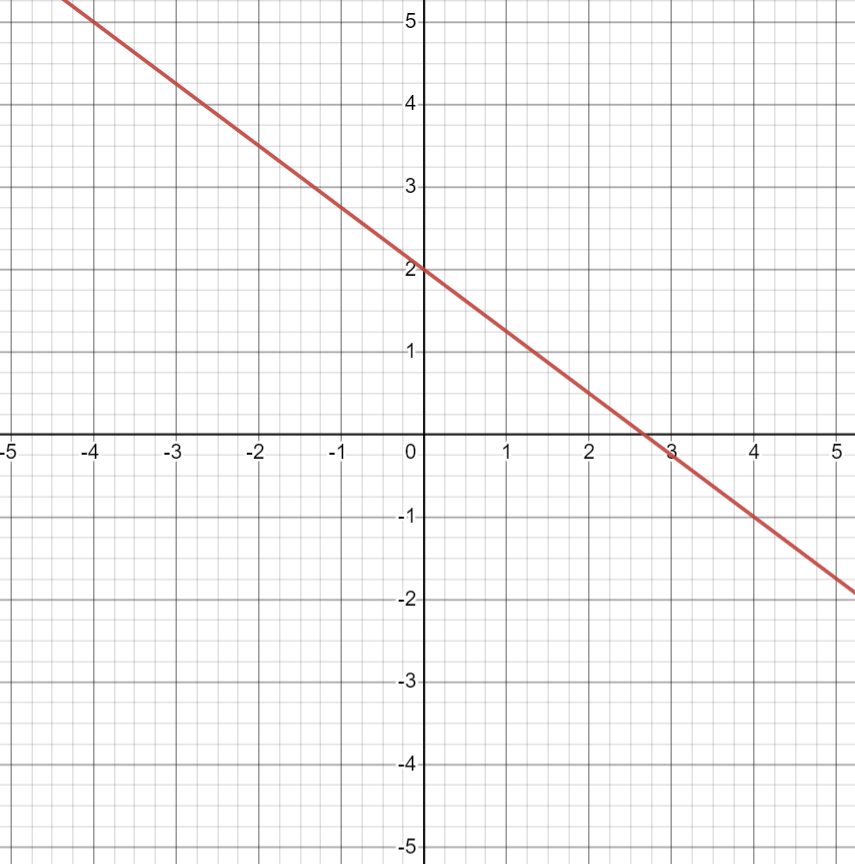 
given line: y= -3/4x+2
parallel: y=-3/4x (+ or - any b value)
perpendicular: y=4/3x (+ or - any b value)