Trigonometry off the Unit Circle
The Unit Circle
The Unit Circle Redux
Angles on the Coordinate Plane
Trig Equations
100
Convert to degrees
(11pi)/20
99 degrees
100
Identify the coordinate on the unit circle for the value
(5pi)/4
(-sqrt(2)/2,-sqrt(2)/2)
100
The quadrant containing points (-x,-y)
Quadrant 3
100
P(4, 1) is a point on the terminal side of \theta in standard form. Find the exact value of
tan\theta write in simplified form
tan\theta=\frac{1}{4}
100
-2+sin\theta=-3
\frac{3\pi}{2}
200
The arc length intercepted by an angle with radius 9 and degree measure of 160.
8\pi or 25.13
200
Find
sin(pi)
0
200
If you have a radian degress measure with a denominator of 6, what angle of a special right triangle should you be referencing?
30
200
(-4,2) is a point on the terminal side of \theta . Find \cos\theta. Write in simplified form.
-\frac{2\sqrt{5}}{5}
200
3-4cos\theta=7-2cos\theta
No solution
300
Find a angle measurement that is coterminal with
\frac{5pi}{3} in radians
Possible answers:
...-\frac{7pi}{3},-\frac{pi}{3},..., \frac{11\pi}{3},\frac{17\pi}{3}...
300
Identify the error with this unit circle.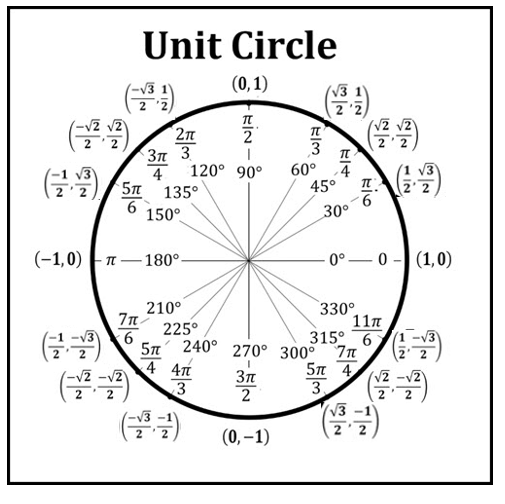
The 30 degree and 60 degree coordinates are switched
300
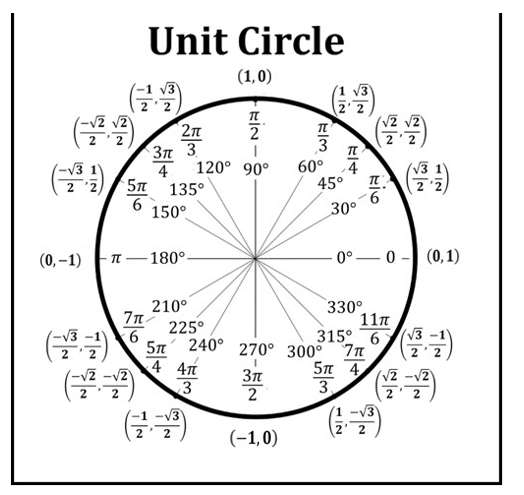
Identify the error in this unit circle
The coordinates of the axes
300
Identify the quadrant where \theta lies if the following statements are true:
cos\theta>0, csc\theta<0
Quadrant IV
300
0=-4-4\sec\theta-sec^2\theta
\frac{2\pi}{3}, \frac{4\pi}{3}
400
Find the area of a sector of a circle that has a radius of 6 meters and a measure of \frac{2\pi}{3} radians.
12\pi or 37.7 m^2
400
Evaluate
sec((-4pi)/3)
-2
400
tan((7pi)/2)
undefined
400
If csc(x)=5/4 and tan(x)<0, find cot(x)
cot\theta=-\frac{3}{4}
400
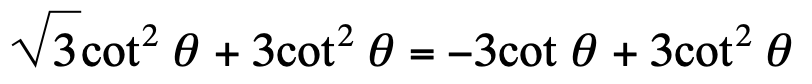
\frac{\pi}{2},\frac{5\pi}{6},\frac{3\pi}{2},\frac{11\pi}{6}
500
If cosine of x is -2/3 and cotangent of x is positive, which quadrant does x lie in?
Quadrant 3
500
\cot(\theta)=-\sqrt{3} for 0°\le\theta<360°
150° and 330°
500
\csc\frac{16\pi}{3}
(-2sqrt(3))/3
500
If secx=-\frac{\sqrt{65}}{4} and csc(x)<0, find tan(x)
\frac{7}{4}
500
\frac{\sin^2x-9){sinx-3)=2
x=\frac{3\pi}{2}