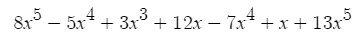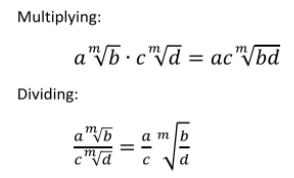Evaluate
Simplify
Rewrite
True/False
Miscellaneous
100
3√(4) * 3√(128)
8
100
21x⁵ - 12x⁴ +3x³ + 13x
100
Rewrite the following in radical form: 2^(2/3)
3√(2 ^ 2)
100
This is the algebraic rule for dividing radicals:
True
100
Solve for x: 42 = (-87 - 4x)6/2
((3√42) + 87)/4
200
√(x+2)=10
x=98
200
7√(10x)/40
200
Rewrite and simplify the following so that the denominator is rationalized: (√3x2y3)/(4√5xy3)
(√15x)/20
200
Does x= 78 satisfy 3(x+3)3/4 = 81?
True/Yes
200
Rewrite the following
10^(17/4)
4√(10^17)
300
√(x+39)+3=1
no solution
300
Simplify the following: 5/(3√10)
(3√100)/2
300
Rewrite the following into exponential form:
4√(8
2^3/4
300
When multiplying two values with the same base, should you subtract the exponential values.
False
300
Solve for x
√(3x+4) = √(2x + 7)
x=3
400
What does √(-1) represent?
i
400
Simplify the following: (2/√(3))^(-4/3)
[3√(36)]/4
400
Rewrite and solve for the following: (2/√(5)) ^ (-4/3)
(√(5)/2) ^ (4/3), [3√(100)]/4
400
Is the following rule correct?:
(a/b)^-n = (b/a)^n
True/Correct
400
Order the following expressions from least to greatest:
√(40/1), √(49/16), √(81/100)
√(81/100), √(46/16), √(40/1)
500
√(2x + 2) + 8 = 0
no solution
500
[77x3 + 45x2 + 3√(46)] / (77x + 7√(46))
(847x4-77√(46x3) + 495x3 - 45√(46x2) + 33√(46x) - 138)/ 7(121x2 - 46)
500
Rewrite and solve for the following: (33√75 + 93√16)/(33√3)
3√25 + 23√18
500
When rationalizing an equation, you multiply both sides by the whole denominator, even if there is a constant being multiplied with the radical.
False
500
What is the x intercept for the following equation when graphed: y=√(x+2)
(-2,0)